High performance computing (HPC) clusters are able to solve big problems using a large number of processors. This is also known as parallel computing, where many processors work simultaneously to produce exceptional computational power and to significantly reduce the total computational time. In such scenarios, scalability or scaling is widely used to indicate the ability of hardware and software to deliver greater computational power when the amount of resources is increased. For HPC clusters, it is important that they are scalable, in other words that the capacity of the whole system can be proportionally increased by adding more hardware. For software, scalability is sometimes referred to as parallelization efficiency — the ratio between the actual speedup and the ideal speedup obtained when using a certain number of processors.
In this post we focus on software scalability and discuss two common types of scaling. The speedup in parallel computing can be straightforwardly defined as
speedup = t1 / tN
where t1 is the computational time for running the software using one processor, and tN is the computational time running the same software with N processors. Ideally, we would like software to have a linear speedup that is equal to the number of processors (speedup = N), as that would mean that every processor would be contributing 100% of its computational power. Unfortunately, this is a very challenging goal for real applications to attain.
Amdahl’s law and strong scaling
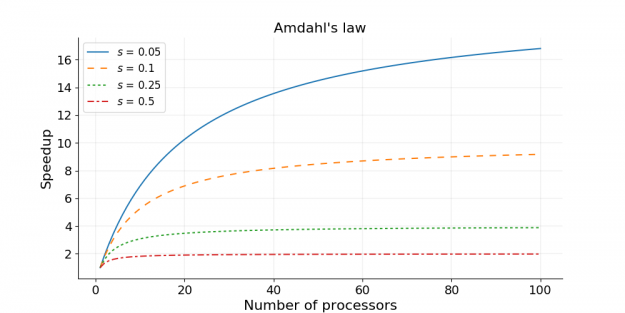
In 1967, Amdahl pointed out that the speedup is limited by the fraction of the serial part of the software that is not amenable to parallelization [1]. Amdahl’s law can be formulated as follows
speedup = 1 / (s + p / N)
where s is the proportion of execution time spent on the serial part, p is the proportion of execution time spent on the part that can be parallelized, and N is the number of processors. Amdahl’s law states that, for a fixed problem, the upper limit of speedup is determined by the serial fraction of the code. This is called strong scaling and can be explained by the following example.
Consider a program that takes 20 hours to run using a single processor core. If a particular part of the program, which takes one hour to execute, cannot be parallelized (s = 1/20 = 0.05), and if the code that takes up the remaining 19 hours of execution time can be parallelized (p = 1 − s = 0.95), then regardless of how many processors are devoted to a parallelized execution of this program, the minimum execution time cannot be less than that critical one hour. Hence, the theoretical speedup is limited to at most 20 times (when N = ∞, speedup = 1/s = 20). As such, the parallelization efficiency decreases as the amount of resources increases. For this reason, parallel computing with many processors is useful only for highly parallelized programs.
Gustafson’s law and weak scaling
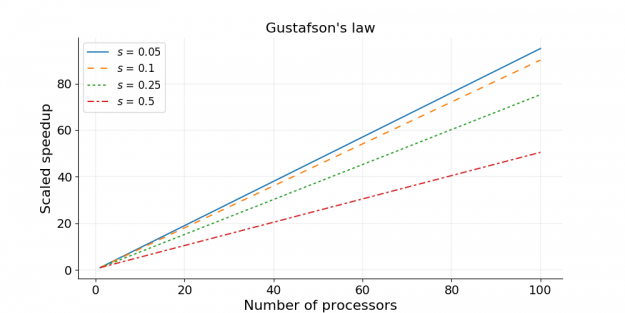
Amdahl’s law gives the upper limit of speedup for a problem of fixed size. This seems to be a bottleneck for parallel computing; if one would like to gain a 500 times speedup on 1000 processors, Amdahl’s law requires that the proportion of serial part cannot exceed 0.1%. However, as Gustafson pointed out [2], in practice the sizes of problems scale with the amount of available resources. If a problem only requires a small amount of resources, it is not beneficial to use a large amount of resources to carry out the computation. A more reasonable choice is to use small amounts of resources for small problems and larger quantities of resources for big problems.
Gustafson’s law [2] was proposed in 1988, and is based on the approximations that the parallel part scales linearly with the amount of resources, and that the serial part does not increase with respect to the size of the problem. It provides the formula for scaled speedup
scaled speedup = s + p × N
where s, p and N have the same meaning as in Amdahl’s law. With Gustafson’s law the scaled speedup increases linearly with respect to the number of processors (with a slope smaller than one), and there is no upper limit for the scaled speedup. This is called weak scaling, where the scaled speedup is calculated based on the amount of work done for a scaled problem size (in contrast to Amdahl’s law which focuses on fixed problem size). If we apply Gustafson’s law to the previous example of s = 0.05 and p = 0.95, the scaled speedup will become infinity when infinitely many processors are used. Realistically, if we have N = 1000, the scaled speedup will be 950.
Measuring parallel scaling performance
When using HPC clusters, it is almost always worthwhile to measure the parallel scaling of your jobs. The measurement of strong scaling is done by testing how the overall computational time of the job scales with the number of processing elements (being either threads or MPI processes), while the test for weak scaling is done by increasing both the job size and the number of processing elements. The results from the parallel scaling tests will provide a good indication of the amount of resources to request for the size of the particular job.
To illustrate the process of measuring parallel scaling, we use an example of OpenMP code, julia_set_openmp.c, which produces an image of a Julia set. A Julia set is associated with a complex function and can be converted to an image by mapping each pixel onto the complex plane. An example of an image for a Julia set is shown below.

The julia_set_openmp.c code contains two OpenMP directives that start with “#pragma omp” (read more about OpenMP syntax from the OpenMP quick reference card). In practice these two “#pragma omp” lines can be merged into one, as shown below. Note that we have added the schedule(dynamic) option, which provides better workload distribution at the cost of some extra overhead. This option also mimics the parallelization overhead in real applications (e.g. communication and load-balancing in MPI-parallelized programs).
# pragma omp parallel for schedule(dynamic) \
shared ( h, w, xl, xr, yb, yt ) \
private ( i, j, k, juliaValue )
for ( j = 0; j < h; j++ )
{
...
}
The main function of julia_set_openmp.c is also modified to accept a height and a width as integer arguments from the command line.
int main ( int argc, char* argv[] )
{
if ( argc < 3 )
{
printf ( "Usage: ./julia_set_openmp height width\n" );
return 0;
}
int h = atoi(argv[1]);
int w = atoi(argv[2]);
...
}
The strong scaling is tested by running the code with different numbers of threads, while keeping the height and width constant. The computational time for generating the Julia set is monitored for each calculation. The results are shown in Table 1 and Figure 1. In Figure 1 we also show the fitted curve based on Amdahl’s law.
The weak scaling is measured by running the code with different numbers of threads and with a correspondingly scaled height. The width was kept constant. The results of the weak scaling test are shown in Table 2 and Figure 2. In Figure 2 we also show the fitted curve based on Gustafson’s law.
Table 1: Strong scaling for Julia set generator code
| height | width | threads | time |
|---|---|---|---|
| 10000 | 2000 | 1 | 3.932 sec |
| 10000 | 2000 | 2 | 2.006 sec |
| 10000 | 2000 | 4 | 1.088 sec |
| 10000 | 2000 | 8 | 0.613 sec |
| 10000 | 2000 | 12 | 0.441 sec |
| 10000 | 2000 | 16 | 0.352 sec |
| 10000 | 2000 | 24 | 0.262 sec |
Table 2: Weak scaling for Julia set generator code
| height | width | threads | time |
|---|---|---|---|
| 10000 | 2000 | 1 | 3.940 sec |
| 20000 | 2000 | 2 | 3.874 sec |
| 40000 | 2000 | 4 | 3.977 sec |
| 80000 | 2000 | 8 | 4.258 sec |
| 120000 | 2000 | 12 | 4.335 sec |
| 160000 | 2000 | 16 | 4.324 sec |
| 240000 | 2000 | 24 | 4.378 sec |
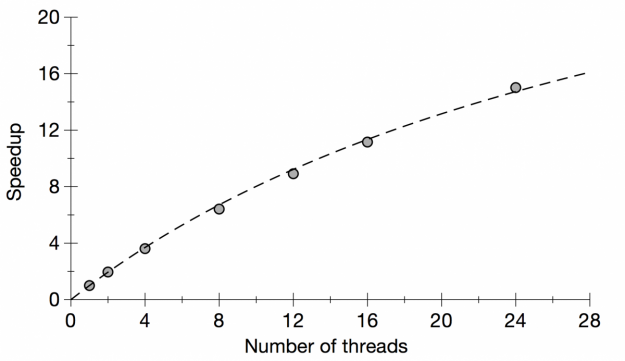
Figure 1: Plot of strong scaling for Julia set generator code
The dashed line shows the fitted curve based on Amdahl’s law.
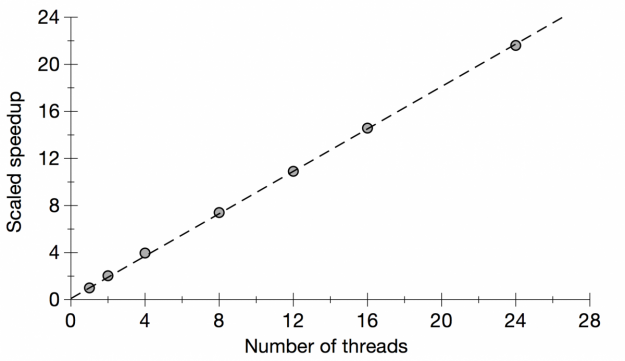
Figure 2: Plot of weak scaling for Julia set generator code
The dashed line shows the fitted curve based on Gustafson’s law.
Based on the formulae for Amdahl’s law and Gustafson’s law, it is possible to fit the strong and weak scaling results and obtain the ratio of the serial part (s) and the parallel part (p). We have done the fitting in Figures 1 and 2, and the fitted value for the serial fraction s is 0.03 for Amdahl’s law and 0.1 for Gustafson’s law. The discrepancy in s is attributed to the approximations in the laws — the serial fraction is assumed to remain constant, and the parallel part is assumed to be sped up in proportion to the number of processing elements (processes/threads). In real applications, the overhead of parallelization may also increase with the job size (e.g. from the dynamic loop scheduling of OpenMP), and in this case it is understandable that the weak scaling test, which involves much larger jobs than those in the strong scaling test, gives a larger serial fraction s.
Summary
This post discusses two common types of scaling of software: strong scaling and weak scaling. Some key points are summarized below.
- Scalability is important for parallel computing to be efficient.
- Strong scaling concerns the speedup for a fixed problem size with respect to the number of processors, and is governed by Amdahl’s law.
- Weak scaling concerns the speedup for a scaled problem size with respect to the number of processors, and is governed by Gustafson’s law.
- When using HPC clusters, it is almost always worthwhile to measure the scaling of your jobs.
- The results of strong and weak scaling tests provide good indications for the best match between job size and the amount of resources that should be requested for a particular job.
References
- Amdahl, Gene M. (1967). AFIPS Conference Proceedings. (30): 483–485. doi: 10.1145/1465482.1465560
- Gustafson, John L. (1988). Communications of the ACM. 31 (5): 532–533. doi: 10.1145/42411.42415

