Parallel programming solves big numerical problems by dividing them into smaller sub-tasks, and hence reduces the overall computational time on multi-processor and/or multi-core machines. Parallel programming is well supported in traditional programming languages like C and FORTRAN, which are suitable for “heavy-duty” computational tasks. Traditionally, Python is considered to not support parallel programming very well, partly because of the global interpreter lock (GIL). However, things have changed over time. Thanks to the development of a rich variety of libraries and packages, the support for parallel programming in Python is now much better.
This post (and the following part) will briefly introduce the multiprocessing module in Python, which effectively side-steps the GIL by using subprocesses instead of threads. The multiprocessing module provides many useful features and is very suitable for symmetric multiprocessing (SMP) and shared memory systems. In this post we focus on the Pool class of the multiprocessing module, which controls a pool of worker processes and supports both synchronous and asynchronous parallel execution.
The Pool class
Creating a Pool object
To use the multiprocessing module, you need to import it first.
import multiprocessing as mp
Documentation for the module can be displayed with the help method.
help(mp)
The module can detect the number of available CPU cores via the cpu_count method. (Note that we use the Python3 syntax for printing the resulting number.)
nprocs = mp.cpu_count()
print(f"Number of CPU cores: {nprocs}")
In practice it is desirable to have one process per CPU core, so it is a good idea to set nprocs to be the number of available CPU cores. A Pool object can be created by passing the desired number of processes to the constructor.
pool = mp.Pool(processes=nprocs)
The map method
To demonstrate the usage of the Pool class, let’s define a simple function that calculates the square of a number.
def square(x):
return x * x
Suppose we want to use the square method to calculate the squares of a list of integers. In serial programming we can use the following code to compute and print the result, via list comprehension.
result = [square(x) for x in range(20)]
print(result)
To execute the computation in parallel, we can use the map method of the Pool class, which is similar to the built-in map function in Python.
result = pool.map(square, range(20))
print(result)
The above parallel code will print exactly the same result as the serial code, but the computations are actually distributed and executed in parallel on the worker processes. The map method will guarantee that the order of the output is correct.
The starmap method
You may have noticed that the map method is only applicable to computational routines that accept a single argument (e.g. the previously defined square function). For routines that accept multiple arguments, the Pool class also provides the starmap method. For example, we can define a more general routine that computes a power of arbitrary order
def power_n(x, n):
return x ** n
and pass this power_n routine and a list of input arguments to the starmap method.
result = pool.starmap(power_n, [(x, 2) for x in range(20)])
print(result)
Note that both map and starmap are synchronous methods. In other words, if a worker process finishes its sub-task very early, it will wait for the other worker processes to finish. This may lead to performance degradation if the workload is not well balanced among the worker processes.
The apply_async method
The Pool class also provides the apply_async method that makes asynchronous execution of the worker processes possible. Unlike the map method, which executes a computational routine over a list of inputs, the apply_async method executes the routine only once. Therefore, in the previous example, we would need to define another routine, power_n_list, that computes the values of a list of numbers raised to a particular power.
def power_n_list(x_list, n):
return [x ** n for x in x_list]
To use the apply_async method, we also need to divide the whole input list range(20) into sub-lists (which are known as slices) and distribute them to the worker processes. The slices can be prepared by the following slice_data method.
def slice_data(data, nprocs):
aver, res = divmod(len(data), nprocs)
nums = []
for proc in range(nprocs):
if proc < res:
nums.append(aver + 1)
else:
nums.append(aver)
count = 0
slices = []
for proc in range(nprocs):
slices.append(data[count: count+nums[proc]])
count += nums[proc]
return slices
Then we can pass the power_n_list routine and the sliced input lists to the apply_async method.
inp_lists = slice_data(range(20), nprocs)
multi_result = [pool.apply_async(power_n_list, (inp, 2)) for inp in inp_lists]
The actual result can be obtained using the get method and nested list comprehension.
result = [x for p in multi_result for x in p.get()]
print(result)
Note that the apply_async method itself does not guarantee the correct order of the output. In the above example, apply_async was used with list comprehension so that the result remained ordered (see also the examples).
Example: computing π
After that brief introduction, we can use the Pool class to do useful things. Here we use the calculation of π as a simple example to demonstrate the parallelization of Python code. The formula for computing π is given below.
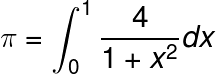
Serial code
With the above formula we can compute the value of π via numerical integration over a large number of points. For example we can choose to use 10 million points. The serial code is shown below.
nsteps = 10000000
dx = 1.0 / nsteps
pi = 0.0
for i in range(nsteps):
x = (i + 0.5) * dx
pi += 4.0 / (1.0 + x * x)
pi *= dx
Parallel code
To parallelize the serial code for computing π, we need to divide the for loop into sub-tasks and distribute them to the worker processes. In other words, we need to evenly distribute the task of evaluating the integrand at 10 million points. This can be conveniently done by providing the start, stop and step arguments to the built-in range function. The first integer in the range function is the start of the sequence, and should be set as the index or rank of the process. The second integer is the number of integration points, namely the end of the sequence. The third integer is the step between the adjacent elements in the sequence, and is set as the number of processes to avoid double counting. For example, the following calc_partial_pi function uses the range function for the sub-task on a worker process.
def calc_partial_pi(rank, nprocs, nsteps, dx):
partial_pi = 0.0
for i in range(rank, nsteps, nprocs):
x = (i + 0.5) * dx
partial_pi += 4.0 / (1.0 + x * x)
partial_pi *= dx
return partial_pi
With the calc_partial_pi function we can prepare the input arguments for the sub-tasks and compute the value of π using the starmap method of the Pool class, as shown below.
nprocs = mp.cpu_count()
inputs = [(rank, nprocs, nsteps, dx) for rank in range(nprocs)]
pool = mp.Pool(processes=nprocs)
result = pool.starmap(calc_partial_pi, inputs)
pi = sum(result)
Asynchronous parallel calculation can be carried out with the apply_async method of the Pool class. We can make use of the calc_partial_pi function and the inputs list since both starmap and apply_async support multiple arguments. The difference is that starmap returns the results from all processes, while apply_async returns the result from a single process. The code using the apply_async method is shown below.
multi_result = [pool.apply_async(calc_partial_pi, inp) for inp in inputs]
result = [p.get() for p in multi_result]
pi = sum(result)
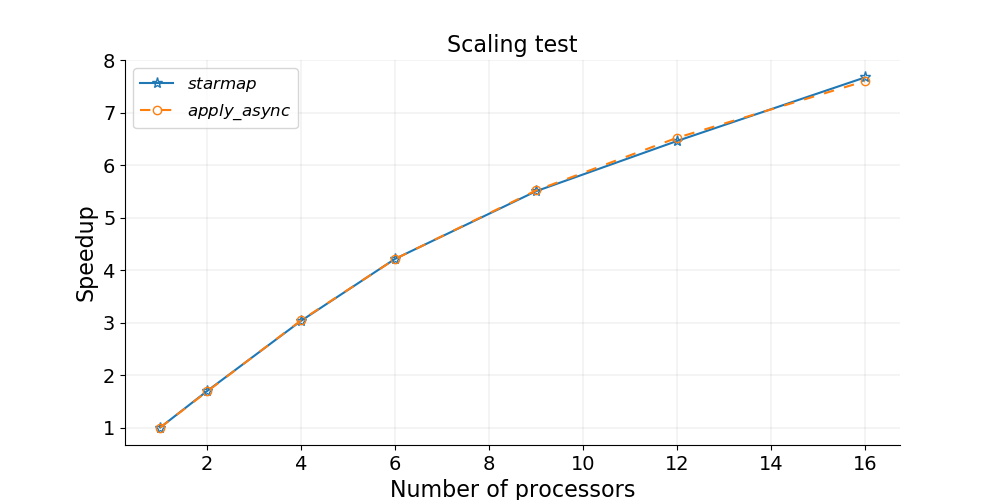
In a previous post we have discussed the scaling of parallel programs. We can also run a scaling test for the parallel Python code based on the starmap and apply_async methods of the Pool class. From the figure below we can see that the two methods provide very similar scaling for computing the value of π.
Summary
We have briefly shown the basics of the map, starmap and apply_async methods from the Pool class.
mapandstarmapare synchronous methods.mapandstarmapguarantee the correct order of output.starmapandapply_asyncsupport multiple arguments.
You may read the Python documentation page for details about other methods in the Pool class.

No comments yet. Be the first to comment!