Kursen använder en lärandefokuserad pedagogik med målinriktade föreläsningar.
ED1110 Vektoranalys 4,5 hp
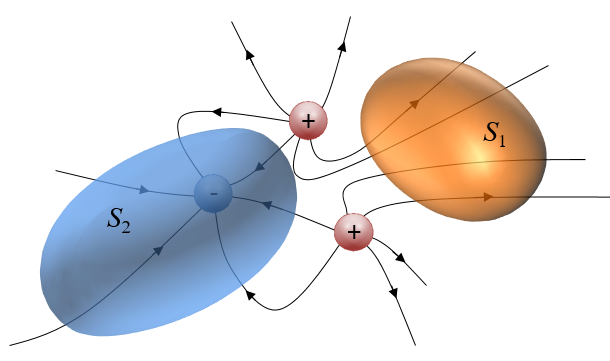
Kursen har som syfte att ge förståelse för de vektoranalytiska sambanden, att visa på praktiska tillämpningar av vektoranalys samt att ge träning i problemformalisering och lösningsmetoder.
Information per kursomgång
Information för HT 2026 Start 2026-08-24 programstuderande
- Studielokalisering
KTH Campus
- Varaktighet
- 2026-08-24 - 2026-10-23
- Perioder
HT 2026: P1 (4.5 hp)
- Studietakt
33%
- Anmälningskod
10745
- Undervisningsform
Normal Dagtid
- Undervisningsspråk
Svenska
- Kurs-PM
- Kurs-PM är inte publicerat
- Antal platser
Min: 1
- Målgrupp
- Sökbar för CELTE, CENMI
- Planerade schemamoduler
- [object Object]
- Schema
- Schema är inte publicerat
- Del av program
Civilingenjörsutbildning i energi och miljö, åk 3, SUT, Villkorligt valfri
Civilingenjörsutbildning i energi och miljö, åk 3, ITH, Villkorligt valfri
Civilingenjörsutbildning i energi och miljö, åk 3, KEM, Villkorligt valfri
Civilingenjörsutbildning i energi och miljö, åk 3, MES, Villkorligt valfri
Civilingenjörsutbildning i energi och miljö, åk 3, ELP, Obligatorisk
Civilingenjörsutbildning i energi och miljö, åk 3, MHI, Villkorligt valfri
Civilingenjörsutbildning i energi och miljö, åk 3, RENE, Villkorligt valfri
Civilingenjörsutbildning i energi och miljö, åk 3, SENS, Obligatorisk
Civilingenjörsutbildning i energi och miljö, åk 3, SMCS, Villkorligt valfri
Civilingenjörsutbildning i energi och miljö, åk 3, HSS, Villkorligt valfri
Civilingenjörsutbildning i energi och miljö, åk 3, SUE, Villkorligt valfri
Civilingenjörsutbildning i elektroteknik, åk 2, Obligatorisk
Kontakt
Kursplan som PDF
Notera: all information från kursplanen visas i tillgängligt format på denna sida.
Kursplan ED1110 (HT 2021–)Innehåll och lärandemål
Kursupplägg
Kursinnehåll
• grundläggande vektoralgebra
• derivering och integration av vektorvärda funktioner i kartesiska, cylindriska och sfäriska koordinatsystem
• gradienten och riktningsderivatan
• potentialen
• linjeintegraler och ytintegraler
• Gauss och Stokes satser
• nablaoperatorn, nablaräkning och indexräkning
• integralsatser
• kroklinjiga koordinatsystem
• viktiga vektorfält och integration av dessa
• Laplaces och Poissons ekvationer.
Lärandemål
Efter godkänd kurs ska studenten kunna
• tillämpa vektoralgebra och använda gradienten av skalärfält för att lösa elementära problem inom fysiken
• utföra linje-, yt- och volymsintegration samt derivering av skalärfält och vektorfält
• fysikaliskt tolka divergensen och rotationen och tillämpa dessa operatorer för att utföra yt- och linjeintegration med hjälp av Gauss och Stokes satser
• identifiera det mest lämpliga koordinatsystemet för ett givet problem och tillämpa gradienten, divergensen och rotationen i det utvalda koordinatsystemet
• använda nablaräkning och indexräkning för att förenkla och utföra vektoranalytiska beräkningar
• lösa Poissons ekvation med lämpliga randvillkor för problem med cylindriska och sfäriska symmetrier
i syfte att få förståelse för vektoranalytiska samband, att visa på praktiska tillämpningar av vektoranalys samt att ge träning i problemformulering och lösningsmetoder.
Kurslitteratur och förberedelser
Särskild behörighet
Kunskaper i envariabelanalys, 7,5 hp, motsvarande slutförd kurs SF1625.
Aktivt deltagande i kursomgång vars slutexamination ännu inte är Ladokrapporterad jämställs med slutförd kurs. Den som är registrerad anses vara aktivt deltagande. Med slutexamination avses både ordinarie examination och det första omexaminationstillfället.
Rekommenderade förkunskaper
Vektoralgebra; addition och subtraktion av vektorer, skalärprodukt, projektion av vektorer, vektorprodukt.
Grundläggande matematisk analyskurs i en och flera variabler.
Kurslitteratur
Examination och slutförande
Betygsskala
Examination
- TENA - Tentamen, 4,5 hp, betygsskala: A, B, C, D, E, FX, F
Examinator beslutar, baserat på rekommendation från KTH:s handläggare av stöd till studenter med funktionsnedsättning, om eventuell anpassad examination för studenter med dokumenterad, varaktig funktionsnedsättning.
Examinator får medge annan examinationsform vid omexamination av enstaka studenter.
När kurs inte längre ges har student möjlighet att examineras under ytterligare två läsår.
Löpande examination används. Den utgörs av hemuppgifter samt individuella uppgifter och gruppuppgifter på övningstid. Tentamen ges också (nödvändig för högre betyg).
Examinator
Etiskt förhållningssätt
- Vid grupparbete har alla i gruppen ansvar för gruppens arbete.
- Vid examination ska varje student ärligt redovisa hjälp som erhållits och källor som använts.
- Vid muntlig examination ska varje student kunna redogöra för hela uppgiften och hela lösningen.
Ytterligare information
Kursrum i Canvas
Ges av
Huvudområde
Utbildningsnivå
Övrig information
I denna kurs tillämpas EECS hederskodex, se:
http://www.kth.se/eecs/utbildning/hederskodex.