Carolin König

Researcher at

Division of Theoretical Chemistry and Biology
Royal Institute of Technology
Roslagstullsbacken 15
S-106 91 Stockholm, Sweden

email: carolink-at-kth.se

Research Interest: Theoretical Spectroscopy of Complex Systems

Spectroscopies of various kinds are essential tools in many areas of natural sciences. The interpretation of experimental spectra of complex systems, however, often requires theoretical input. Theoretical spectroscopy can often provide an understanding on an atomistic level that cannot be reached by experiment alone. The reliable spectra simulations of complex systems by means of quantum-chemical methods, are, however, far from trivial and novel computational approaches are needed to provide a reliable theoretical support.

My main research interest and expertise lie in the development and application of efficient methods in theoretical spectroscopies to complex systems, where my focus lies on optical and vibrational spectroscopy of bio-systems. Recently, I am also working on noble metal nanoparticle systems.

1) Flourescent Biomarkers for Amyloid Fibrils

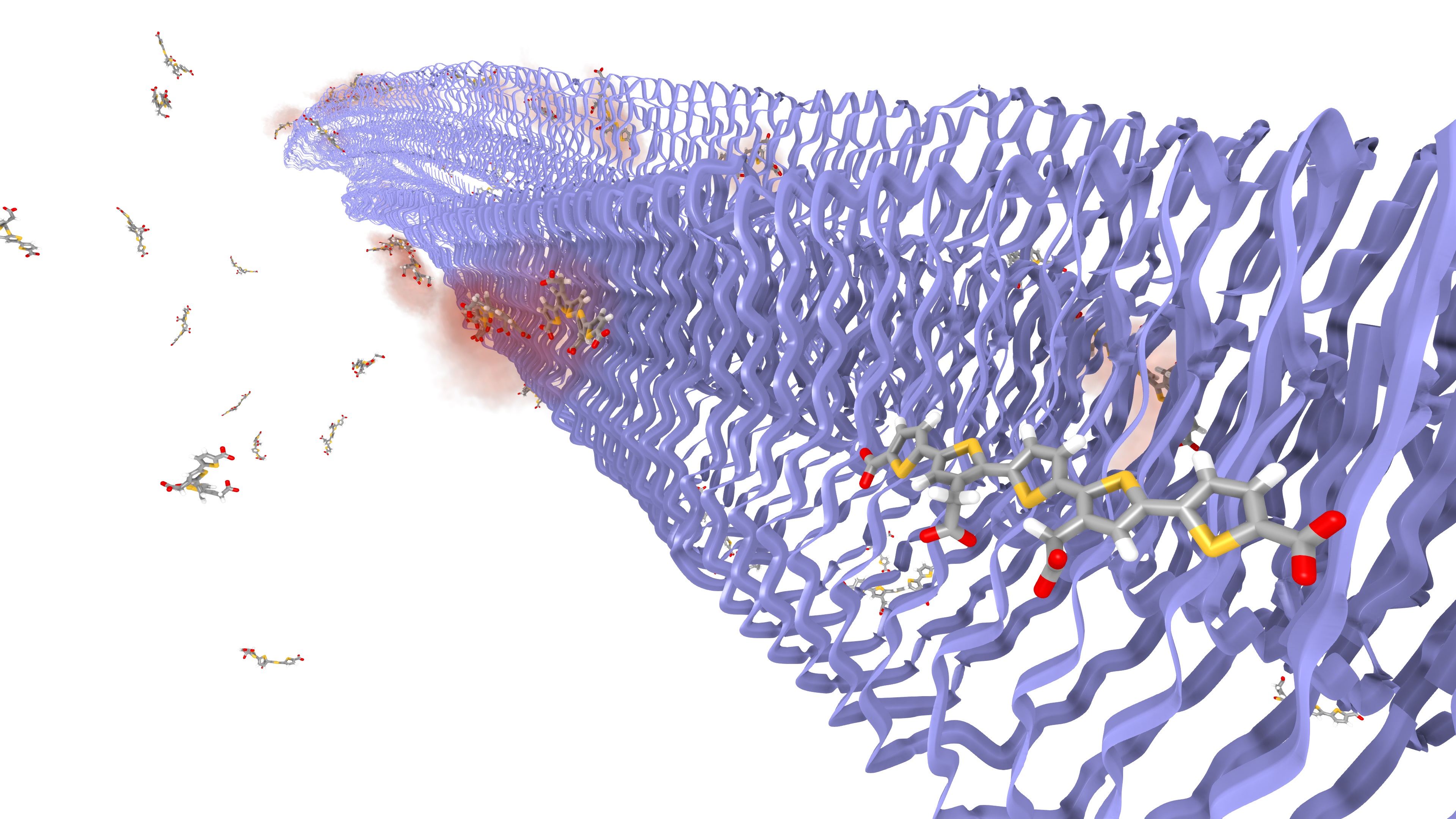
Luminescent conjugated oligothiophenes are highl y promising candidates for biomarkers for amyloid misfolds and thereby for early-stage detection of neurodegenerative diseases such as Alzheimer’s and Parkinson's disease. The elucidation of the microscopic mechanism and design principles behind these biomarkers requires theoreticalassi stance. Finding suitable theoretical models that allow sufficiently accurate spectra calculations for such large, dynamic, and complex biomolecular systems is a highly challenging task. There is, hence, a great need for efficient and adaptive theoretical models capable of incorporating the essential factors in spectra calculationof biomolecular systems sufficiently accurately.
We aim at combining the advantages of different state-of-the-art computational methods and thereby to devise an efficient and adaptable methodology for assisting the interpretation of existing spectra and predicting the performance of new candidates for biomarkers with respect to spectral discrimination of amyloid protein misfolds and thereby for improved early-stage detection and more nuanced diagnosis of diseases such as Alzheimer’s and Parkinson’s disease. This project is founded by a Marie-Sklodowska-Curie Individual Fellowship by the European Commission.

As a first step to this goal, we have performed large-scale non-biased molecular dynamics simulations of an amyloid fibril in the presence of luminescent biomarkers. In these simulations, we succeeded in finding a convincing binding site for a luminescent oligothiophene biomarkers, which is in agreement with current experimental results.

[1] C König, R Skånberg, I Hotz, A Ynnerman, P Norman, and M Linares, Binding Sites for Luminescent Amyloid Biomarkers from non-Biased Molecular Dynamics Simulations, Chem. Commun., 54, 3030-3033 (2018).

2) Local approaches in vibrational structure theory

Vibrational spectra of complex systems, such as proteins, are very sensitive to structural changes of the investigated molecules.  The interpretation of these spectra, however, requires theoretical assistanc and the most standard harmonic approximation does often leave ambiguities.  In vibrational structure theory we go beyond the harmonic approximation and use vibrational wave functions in anharmonic potential energy surfaces to calculate optical spectra. These calculations are, however, considerable more demanding and exhibit steeper computational scaling than the standard harmonic choice. This restricts the applicability of the standard models to a few tens of vibrational modes. Especially for larger systems, we expect that the locality of the interaction within a system can be exploited to devise highly efficient vibrational structure approaches. With these developments we expect to push the size limitations of these methods to much larger system sizes.

My work in this field comprises all three components, i.e., the vibrational coordinates, the generation of the potential energy surface as well as the parameterization of the vibrational wave function itself. Examples of my work on the first two aspects can be found below. The software platform of these projects is the MidasCpp code by the group of Ove Christiansen at Aarhus University, which I am collaborating with.

2a) Local vibrational coordinates

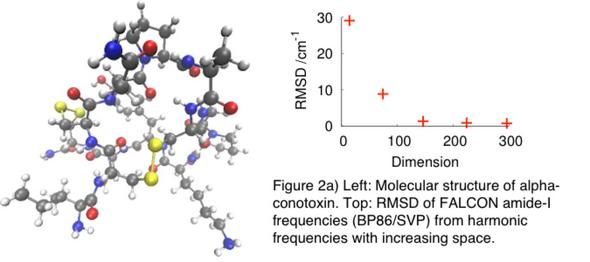
My work in the generation of alternative vibrational coordinates includes the combination of localization and optimization schemes for rectilinear vibrational coordinates[1] as well as the so-called flexible adaptation of local coordinates of nuclei (FALCON). The latter FALCON-type coordinates are due to their well-defined spatial locality key ingredients for the efficient generation of PESs in the double incremental approach described in 2b. The FALCON scheme can furthermore been used to generate spatially motivated vibrational subspaces that can be expanded systematically. We could, for example, show that for alpha-conotoxin a subspace of 146 strictly local modes (out of the total space of 519 vibrations) is capable of approximating the full harmonic solutions with an error that is clearly below the errors expected from other error sources.

[2] E.L. Klinting, C. König, and O. Christiansen, Hybrid Optimized and Localized Vibrational Coordinates, J. Phys. Chem. A, 119, 11007-11021 (2015).

[3] C. König, M.B. Hansen, I.H. Godtliebsen, and O. Christiansen, FALCON: A Method for Flexible Adaptation of Local Coordinates of Nuclei, J. Chem. Phys., 144, 074108 (2016).

2b) Fragmented description of the potential energy surface

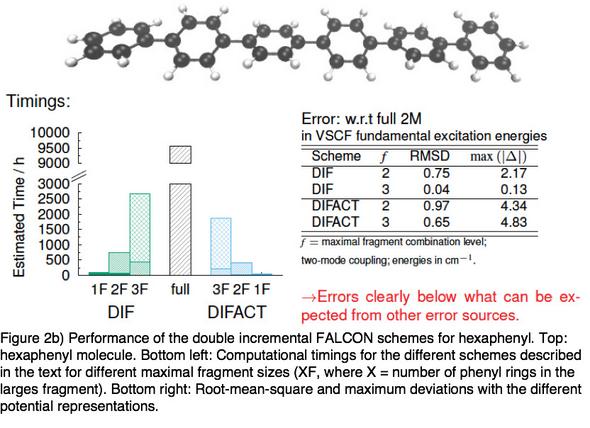
We have shown that the so-called double incremental expansion in combination with the above-mentioned FALCON coordinates (DIF) can be used to devise a computationally highly efficient scheme for PES generations. Adding an approximate transformation step for the some of the vibrational coordinates in the PES (DIFACT), even linear scaling of the accumulated cost for all single-point calculations in the PES generation can be achieved.

This work pushes the previous size limitations for PES generations from quantum-chemical electronic energy points to significantly larger systems. This means that vibrational structure calculations for covalently bound systems with several hundreds of degrees of freedom are now within reach: In the hexa-phenyl case, we treated all 180 vibrational degrees of freedom explicitly in the PES as well as in the anharmonic vibrational calculations including infrared spectra.

[4] C. König and O. Christiansen, Linear-Scaling Generation of Potential Energy Surfaces Using a Double Incremental Expansion, J. Chem. Phys., 145, 064105 (2016).

[5] D. Madsen, O. Christiansen, and C. König, Anharmonic Vibrational Spectra from Double Incremental Potential Energy and Dipole Surfaces, Phys. Chem. Chem. Phys., 20,3445-3456  (2018).

3) Density-based embedding approaches for optical spectroscopy

Standard quantum-chemical methods exhibit steep computational scaling with system size and can therefore not be applied to large bio-molecular systems. Motivated by the local nature of many properties, a plethora approaches dividing the total system into smaller subsystems have been suggested with the multi-level quantum mechanics in molecular mechanics (QM/MM) approach being the most prominent one, which treat part of the system classically. A full quantum-chemical, but still fragmented description can be achieved by more rigorous density-based embedding, such as the so-called Frozen Density Embedding (FDE) scheme.

During my PhD studies, I have developed FDE schemes with a view on optical spectra calculations, both on local excitations and delocalized, coupled excitations as described below. This work has been performed in the group of Johannes Neugebauer.

3a) Tamm–Dancoff Approximation in coupled Frozen Density Embedding

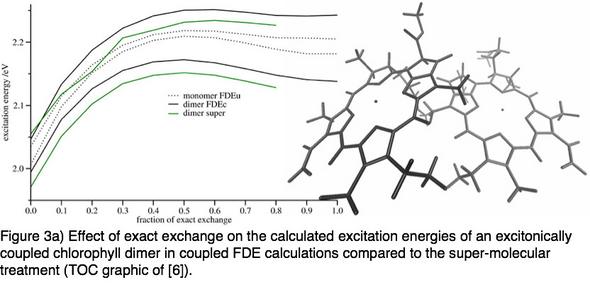
The original formulation of coupled FDE has been formulated for full time-dependent density functional theory (TDDFT) applicable for pure density functionals only. I have re-derived the coupled FDE formalism in a density matrix formalism and thereby introduced the so-called Tamm–Dancoff Approximation (TDA) to the coupled FDE scheme.[5] Using this approximation the excitonic couplings are directly accessible. By introducing the TDA approximation to the coupled FDE, we have furthermore opened the possibility to include exact exchange in the local part of this scheme. This contribution is well known to be essential for the accuracy of certain excitations within the TDDFT framework. The new development allowed us to investigate different exciton coupling mechanisms.[6]

[6] C. König, N. Schlüter, and J. Neugebauer, Direct Determination of Exciton Couplings from Subsystem Time-Dependent Density-Functional Theory within the Tamm-Dancoff Approximation, J. Chem. Phys., 138, 034104 (2013).

[7] C. König and J. Neugebauer, Exciton Coupling Mechanisms Analyzed with Subsystem TDDFT: Direct vs Pseudo Exchange Effects, J. Phys. Chem. B, 117, 3480-3487 (2013).

3b) State-specific density embedding for excited state

In the standard formulation, FDE response theory for local excitation energies neglects the response of the environmental electron density upon the excitation of the embedded dye. We have theoretically and computationally shown how to include this differential polarization effect by means of state-specific embedding potentials. We have tested this methodology for different wave function methods as well as ways to generate the excited state electron density. This was done in collaboration with the group of Claudia Filippi at University of Twente.

[8] C. Daday, C. König, O. Valsson, J. Neugebauer, and C. Filippi, State-Specific Embedding Potentials for Excitation-Energy Calculations, J. Chem. Theory Comput., 9, 2355-2367 (2013).

[9] C. Daday, C. König, J. Neugebauer, and C. Filippi, Wavefunction-in-Density Functional Theory Embedding for Excited States: Which Wavefunctions, which Densities?, ChemPhysChem, 15, 3205-3217 (2014).

4) Subsystem-based quantum chemistry for photosynthetic light harvesting

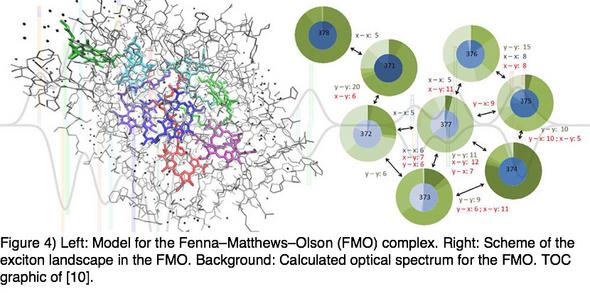
During my PhD studies have applied FDE methods for spectra calculations for different natural light-harvesting complexes, i.e., the Fenna–Matthews–Olson (FMO) protein and the light-harvesting complex II (LHC-II). In the LHC-II study, we have investigated the effects of different aspects of the model setup on the calculated spectra and have furthermore simulated mutagenesis studies.[9] Our results were in qualitative agreement with the experimental counterparts. They could further shed light on the role of individual pigments in the pigment aggregate. The largest model for the FMO protein comprised more than 7000 atoms; all treated in terms of density functional theory. This study has thereby shown the potential of subsystem DFT for application to systems with several thousands of atoms. In this latter work, we were able to give a detailed picture of the excitonic landscape with a nearly complete FMO model. See also our comprehensive review article on the Quantum Chemical Description of Absorption Properties and Excited-State Processes in Photosynthetic Systems.

[10] C. König and J. Neugebauer, First-Principles Calculation of Electronic Spectra of Light-Harvesting Complex II, Phys. Chem. Chem. Phys., 13, 10475-10490 (2011).

[11] C König and J. Neugebauer, Protein Effects on the Optical Spectrum of the Fenna-Matthews-Olson Complex from Fully Quantum Chemical Calculations, J. Chem. Theory Comput., 9, 1808-1820 (2013).

[12] C. König and J. Neugebauer, Quantum Chemical Description of Absorption Properties and Excited-State Processes in Photosynthetic Systems, ChemPhysChem, 13, 386-425 (2012).

5) Improved theoretical models for plasmons in noble metal nanoparticles

The support of surface plasmons (collective electron oscillations) and the accompanying unique features of noble metal nanoparticles make them very promising candidates for applications in many areas of societal interest, such as health care and energy conversion. The theoretical description of these effects, is, however, hampered by the intermediate size of the nanoparticles: On the one hand, established quantum-chemical methods for small system sizes are computationally to demanding to treat nanoparticles with several thousands of metal atoms. On the other hand the available methods for bulk systems typically rely on periodic boundary conditions and can therefore not describe size-dependent effects, as they are observed for nanoparticles.

I am currently working together with Hans Ågren, Zilvinas Rinkevicius, and Jaime A Rosal Sandberg on theoretical models providing an improved description of plasmons in noble metal nanoparticles.