Covariant and invariant receptive fields under natural image transformations

When a visual agent observes three-dimensional objects in the world by a two-dimensional light sensor (retina), the image data will be subject to basic image transformations in terms of:

• local scaling transformations caused by objects of different size and at different distances to the observer,
• local affine image deformations caused by variations in the viewing direction relative to the object,
• local Galilean transformations caused by relative motions between the object and the observer, and
• local multiplicative intensity transformations caused by illumination variations.

Nevertheless, we perceive the world as stable and use visual perception based on brightness patterns for inferring properties of objects in the surrounding world.

We have developed a general framework for handling such inherent variabilities in visual data because of natural image transformations and for computing covariant and invariant (stable) visual representations under these:

• Lindeberg (2021) "Normative theory of visual receptive fields", Heliyon 7(1): e05897: 1-20. (Download PDF)
• Lindeberg (2023) "Covariance properties under natural image transformations for the generalized Gaussian derivative model for visual receptive fields", Frontiers in Computational Neuroscience 17: 1189949: 1-23. (Download PDF)
• Lindeberg (2024) "Do the receptive fields in the primary visual cortex span a variability over the degree of elongation of the receptive fields?", arXiv preprint arXiv:2404.04858. (Download PDF)
• Lindeberg (2024) "Orientation selectivity properties for the affine Gaussian derivative and the affine Gabor models for visual receptive fields", arXiv preprint arXiv:2304.11920. (Download PDF)
• Lindeberg (2013) "Invariance of visual operations at the level of receptive fields", PLOS ONE, 8(7): e66990:1-33. (Download PDF)
• Lindeberg (2013) ''A computational theory of visual receptive fields'', Biological Cybernetics, 107(6): 589-635. (Download PDF)
• Lindeberg (2013) "Generalized axiomatic scale-space theory", Advances in Imaging and Electron Physics, 178: 1-96. (Download PDF)
• Lindeberg (2016) "Time-causal and time-recursive spatio-temporal receptive fields", Journal of Mathematical Imaging and Vision, 55(1): 50-88. (Download PDF) (Video recorded survey talk)

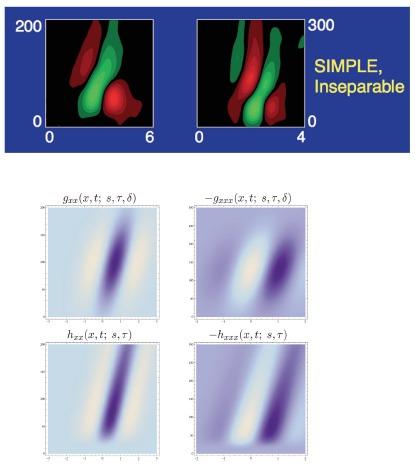
Based on symmetry properties of the environment and additional assumptions regarding the internal structure of computations of an idealized vision system, we have formulated a normative theory for visual receptive fields and shown that it is possible to derive families of idealized receptive fields from a requirement that the vision system must have the ability of computing covariant or invariant image representations under natural image transformations.

There are very close similarities between the receptive fields predicted from our theory and receptive fields found by cell recordings in mammalian vision, including (i) spatial on-center-off-surround and off-center-on-surround receptive fields in the retina and the LGN, (ii) simple cells with spatial orientation preference in V1, (iii) spatio-chromatic double-opponent cells in V1, (iv) space-time separable spatio-temporal receptive fields in the LGN and V1 and (v) non-separable space-time tilted receptive fields in V1.

Thereby, our theory shows that it is possible to predict properties of visual neurons from a principled axiomatic theory. The receptive field families generated by this theory can also constitute a general basis for expressing visual operations for computational modelling of visual processes and for computer vision algorithms.

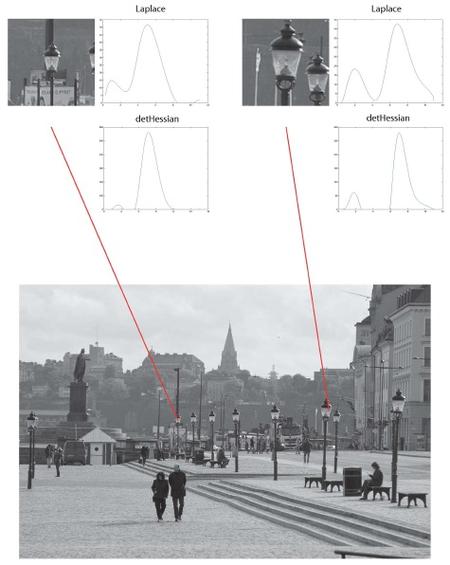
Specifically, our notions of scale selection based on local extrema over scale of scale-normalized derivative responses, and affine or Galilean normalization by affine shape adaptation or Galilean velocity adaptation, alternatively by detecting affine invariant or Galilean invariant fixed points over filter families in affine or spatio-temporal scale space, provides a general framework for computing scale invariant, affine invariant and Galilean invariant image features and image descriptors both for generic purposes in computer vision and as plausible mechanisms for achieving invariance to natural image transformations in computational models of biological vision.