Normative theory for auditory receptive fields
The information in sound is carried by variations in the air pressure over time, which for many sound sources can be modelled as the superposition of sine wave oscillations of different frequencies. To capture this information by auditory perception or signal processing, the sound signal must be processed over some non-infinitesimal amount of time and in the case of a spectral analysis also over some range of frequencies. Such a region over time or over the spectro-temporal domain is referred to as a temporal or spectro-temporal receptive field.
If one considers the theoretical or algorithmic problem of designing an auditory system that is going to analyse the variations in air pressure over time, one may ask what types of auditory operations should be performed on the sound signal. Would any operation be reasonable? Specifically, regarding the notion of receptive fields, what types of temporal or spectro-temporal receptive field profiles would be reasonable? Is it possible to derive a theoretical model of how receptive fields "ought to" respond to auditory signals.
By developing a scale-space theory for auditory signals, we have shown how it is possible to develop a normative theory for receptive fields over auditory signals, and how idealized computational models of auditory receptive fields can be defined in a principled manner:
- Lindeberg and Friberg (2015) "Idealized computational models of auditory receptive fields", PLOS ONE, 10(3): e0119032:1-58. (Download PDF)
- Lindeberg and Friberg (2015) "Scale-space theory for auditory signals", Proc. SSVM 2015: Scale-Space and Variational Methods in Computer Vision, Springer LNCS 9087: 3-15. (Download PDF)
- Lindeberg (2025) "A time-causal and time-recursive analogue of the Gabor transform", IEEE Transactions on Information Theory, 71(2): 1450-1480. (Download PDF)
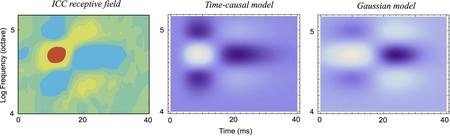
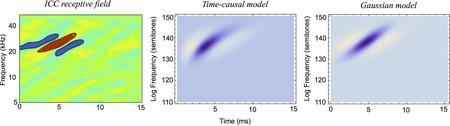
When applied to the definition of spectrograms, alternatively to the formulation of an idealized cochlea model, our scale-space approach can be used for deriving the Gabor and Gammatone approaches for computing local windowed Fourier transforms as specific cases of a complex-valued scale-space transform over different frequencies. Additionally, our scale-space approach to defining spectrograms leads to a new family of generalized Gammatone filters, where the time constants of the individual first-order integrators coupled in cascade are not equal as for regular Gammatone filters but instead distributed logarithmically over temporal scales, and allowing for different trade-offs in terms of e.g. the frequency selectivity of the spectrogram and the temporal delay of time-causal receptive fields.
When applied to a logarithmic transformation of the spectrogram, as motivated from the desire of handling sound signals of different strength (sound pressure) in an invariant manner and with a logarithmic transformation of the frequencies as motivated by the desire of enabling invariance properties under a frequency shift, such as transposing a musical piece by one octave, this theory also allows for the definition of spectro-temporal receptive fields at higher levels in the auditory hierarchy in terms of spectro-temporal derivatives of spectro-temporal smoothing functions as obtained from scale-space theory.

Such second-layer receptive fields can be used for computing basic auditory features such as onset detection, partial tone enhancement and formants, and specifically includes the possibility of defining different types of features at different temporal scales, logspectral scales as well as a glissando parameter that represents how logarithmic frequencies may vary over time.
By built-in covariance properties of our model under temporal shifts, variations in sound pressure, frequency shifts and glissando transformations, the proposed approach allows for provable invariance properties under natural transformations of sound signals.
Specifically, the theory leads to predictions of auditory receptive fields that are qualitatively similar to biological receptive fields as measured by cell recordings in the inferior colliculus (ICC) and the primary auditory cortex (A1) (see figures below).