Till KTH:s startsida Till KTH:s startsida

Vektoranalys

Logga in till din kurswebb

Du är inte inloggad på KTH så innehållet är inte anpassat efter dina val.

Från och med den 1 juni 2025 upphör möjligheten att redigera innehåll i kurswebben och studenter slutar bli inlagda. Redan existerande material kvarstår.

Läs mer här: Kurswebbens solnedgång den första juni

BASIC INFORMATION

INTRODUKTION

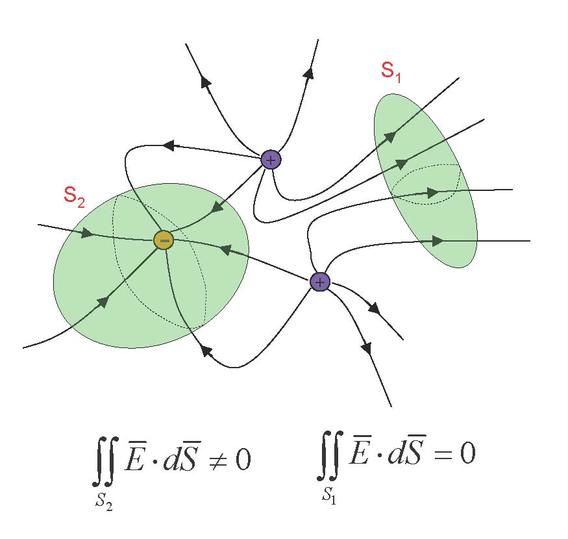
gauss

Inom geometrin och mekaniken utgör vektorer (storheter med både storlek och riktning) mycket användbara verktyg. Vidare kan nya vektorer bildas med hjälp av addition, subtraktion, skalärmultiplikation eller kryssprodukt av gamla.

  • Ibland kan man ha behov av att bestämma hur en vektorstorhet varierar i rummet eller tiden, dvs man intresserar sig för dess derivata. Vektoranalys behandlar just derivator och integraler av vektorer.
  • Metoderna inom vektoranalysen kan formuleras inom flervariabelsanalysen, men vektoranalysen har mycket större praktisk användbarhet eftersom den tillåter mer komprimerade och intuitiva formuleringar.
  • Det visar sig att vektoranalys är mycket användbar inom ämnen som teoretisk elektroteknik, vågrörelselära, strömningsmekanik, plasmafysik, gasdynamik och relativitetsteori.
Anmäl missbruk

Lärare