Research
Selected research work by Jan Scheffel, with brief summaries
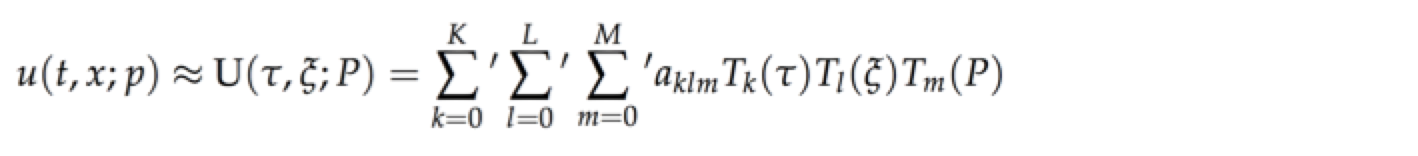
COMPUTATIONAL PHYSICS - SOLUTION OF ODEs AND PDEs
• A Spectral Method in Time for Initial-Value Problems
Am. J. Comp. Math Vol.2 No.3, pp. 173-193, 2012.
• A time-spectral approach to numerical weather prediction
Computer Physics Communications, vol. 226, pp. 127-135, 2018.
• Optimizing Time-Spectral Solution of Initial-Value Problems
Am. J. Comp. Math, vol. 8, pp. 7-26, 2018.
Summary: These papers outline a novel time-spectral method as an alternative to finite differencing for solution of time-dependent ordinary and partial differential equations in physics. Semi-analytical solutions in terms of Chebyshev series are obtained. The CFL condition and other grid causality conditions associated with time marching algorithms are eliminated. High efficiency and accuracy are obtained by innovative algorithms for temporal and spatial subdomains in combination with sparse matrix methods. The method is termed the
Generalized Weighted Residual Method (GWRM).
COMPUTATIONAL PHYSICS - SOLUTION OF ALGEBRAIC EQUATIONS
• Solution of Systems of Equations - a Semi-implicit Approach
Applied Numerical Mathematics, Volume 59, Issue 10, pp. 2430-2443, 2009.
• SIR - an efficient root solver for systems of nonlinear equations
Software Quality Professional, vol. 7, s. 59-62, 2018.
Summary: The Semi-Implicit Root solver (SIR) is an iterative method for globally convergent solution of systems of nonlinear equations. SIR convergence is quasi-monotonous and approaches second order in the proximity of the real roots. Global convergence is usually superior to that of Newton's method, being a special case of the method. The algorithm
cannot land on local minima, as may be the case for Newton's method with line search.
OPERATIONAL LIMITS OF FUSION CONFIGURATIONS
• Effect of Thermal Conduction on Pressure-driven Modes in the Reversed-field Pinch
Nuclear Fusion, vol. 52, no. 12, s. 123012, 2012.
Summary: In this study, it is shown that linear stability of pressure driven resistive modes in the reversed-field pinch (RFP) require kinetic effects, such as finite Larmor radius stabilization. Classical linearized resistive magnetohydrodynamic (MHD) stability theory predicts unstable pressure-driven modes even at low plasma pressure for the RFP. Including also allegedly stabilizing thermal conduction effects we here show that pressure-driven resistive g-modes are stabilized only for very low values of plasma pressure.
• Confinement Scaling Laws for the Conventional Reversed-field Pinch
Physical Review Letters, vol. 85, no. 2, s. 322-325, 2000.
Summary: We have here, for the first time, determined theoretical limits for RFP confinement behaviour. The results indicate significant degradation from the standard picture of RFP confinement, but are in good agreement with experimental results. They emphasize the importance of experimentally demonstrating control of the RFP current profile in order to improve energy confinement. A series of high resolution, 3D, resistive MHD numerical simulations of the reversed-field pinch are performed to obtain scaling laws for poloidal beta and energy confinement at Lundquist numbers approaching 10**6. Optimum plasma conditions are attained by taking the transport coefficients to be classical, and by ignoring radiation losses and resistive wall effects. We find that poloidal beta scales as I**(-0.40) and that the energy confinement time scales as I**0.34 for fixed I/N, with aspect ratio 1.25. I is the plasma current.
• Numerical Studies of Confinement Scalings for the Dynamo Free Reversed-field Pinch
Nuclear Fusion, vol. 47, no. 1, s. 9-16, 2007.
Summary: In the RFP, tearing modes associated with the dynamo fluctuations are responsible for reduced energy- and particle confinement. In this numerical study, it is observed that by implementing current profile control (CPC) in the RFP, a dynamo-free state can be achieved. Scaling laws are determined for radial magnetic field, energy confinement time, poloidal beta and temperature. Confinement is improved substantially as compared with the conventional RFP - the temperature reaches reactor relevant levels by ohmic heating alone. The focus of this study is on obtaining principal theoretical optimization of confinement in the RFP by implementing CPC, thus investigating the reactor viability of the concept.
• Large Larmor Radius Stability of the Z-pinch
Physical Review Letters, vol. 72, s. 2399, 1994.
Summary: This is the first theoretical evidence that kinetic finite Larmor radius effects cannot in themselves produce a stabilized zpinch. The linear m = 0 stability of the z pinch in the collisionless, large ion Larmor radius regime is examined using the Vlasov fluid model. The results reveal a strong equilibrium dependence. The uniform current density equilibrium shows a reduction in growth rate when the average ion Larmor radius is about one-fifth of the pinch radius. Complete stabilization of m = 0 modes is only achieved in unphysical cases where the pressure is relatively high at the plasma boundary.
• Linear Stability of the High Temperature, Dense Z-pinch
Physical Review Letters, vol. 74, s. 2698, 1995.
Summary: Results are presented on the linear stability of the collisionless m = 1 mode in a dense zpinch. It is shown that a reduction in growth rate by a factor of about 10 (when compared to the zero Larmor radius result) is possible by initializing the zpinch with a sufficiently low line density. With the completion of this work we conclude that linear, large Larmor radius effects cannot stabilize the high temperature, dense zpinch. Such pinches will always exhibit linear m = 0 or m = 1 instabilities with growth times comparable to the radial Alfvén transit time.
FUNDAMENTAL PHYSICS
• Large Debye Distance Effects in a Homogeneous Plasma
Journal of Plasma Physics, vol. 41, s. 493, 1989.
Summary: The classical phenomenon of electron plasma oscillations is investigated from new aspects. It is found, for the first time, that the mixing effect of large electron excursions, as compared to the Debye length, introduces significant damping. The corresponding large-Debye-distance (LDD) damping is found to substantially dominate over Landau damping. This limits the applicability of normal-mode analysis of Maxwellian and non-Maxwellian distributions. The physics of LDD damping and its close connection to large-Larmor-radius (LLR) damping is discussed. A major finding concerns perturbations of plasmas with non-Maxwellian, bump-in-tail, velocity distribution functions f0(w). For sufficiently large αλD (of order unity) the plasma responds by damping perturbations that are initially unstable in the Landau sense, i.e. with phase velocities initially in the interval where df0/dw > 0.
• On the Minimum Elementary Charge of an Extended Electromagnetic Theory
Physica Scripta, vol. 65, no. 3, s. 200-207, 2002.
Summary: In this study it is argued that the electronic charge should not be considered as an independent constant of nature, but can be deduced in terms of the velocity of light and Planck's constant. Steady axisymmetric equilibria of an earlier developed extended electromagnetic theory are considered, as based on a nonzero electric field divergence in the vacuum state and Lorentz invariance. The computed value of the electron charge deviates only by about 3 percent from that of the experimentally determined elementary charge, and it depends only on the velocity of light and Planck's constant.
