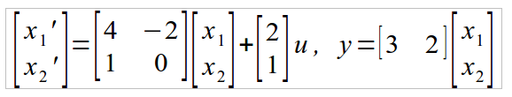Seminarier

Under kursen ges tre seminarieövningar med uppgifter enligt nedan. Alla dessa uppgifter ska lösas innan respektive seminarie, vid seminariet väljs slumpvis vilka som ska redovisa vilka uppgifter. Varje godkänt seminarie ger en godkänd uppgift (värd 2 poäng) på tentamen. Detta gäller endast ordinarie tentamen.

Seminarie 1

6.9b,d, 7.5b, 7.9, 7.17d, 8.5f, 9.11, 10.9, 10.11, 10.20, 11.6

Seminarie 2

16.5d, 16.6b, 17.1b, 17.9 (tillåtet använda matlab), 18.4b, 18.6e, 18.9a, 19.6a, 19.7b

Seminarie 3

Det är tillåtet att använda Matlab för matrisberäkningar.

14.1d, 14,3b-Räkna även ut var systemets poler ligger och avgör om det är stabilt, 14.4c, 14.6b, 14.9, nedanstående uppgift:
Nedanstående process ska regleras med en polplaceringsregulator, alla poler ska ligga i s = -0,40. Rita ett blockschema med uträknade värden (L ock Kr) för regulatorn.

Ska det inte vara [x1; x2] multiplicerat med [4 -2; 1 0], likt bilden nedan?

$$\begin{bmatrix} {x_{1}}^{'} \\ {x_{2}}^{'} \end{bmatrix} = \begin{bmatrix} 4 & -2 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} + \begin{bmatrix} 2 \\ 1 \end{bmatrix} u, y = \begin{bmatrix} 3 & 2 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}$$

Blev lite fundersam när jag skulle räkna uppgiften. Har räknat med [x1; x2] nämligen, men ser att det faktiskt inte finns med i uppgiftsbilden.

(Tänkte att ekvationen var på formen x' = Ax + Bu)