Research, computational physics

Selected research work by Jan Scheffel, with brief summaries

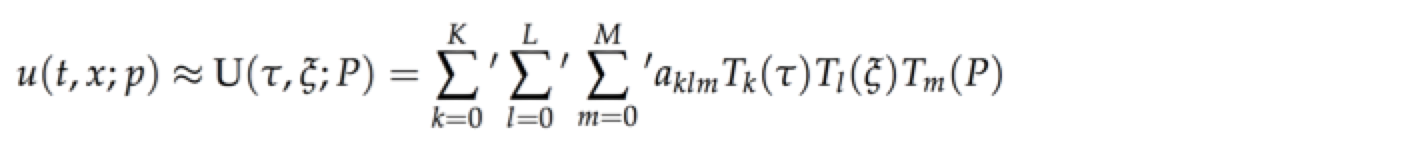
COMPUTATIONAL PHYSICS - SOLUTION OF ODEs AND PDEs
• A Spectral Method in Time for Initial-Value Problems 
Am. J. Comp. Math Vol.2 No.3, pp. 173-193, 2012.
• A time-spectral approach to numerical weather prediction 
Computer Physics Communications, vol. 226, pp. 127-135, 2018.
• Optimizing Time-Spectral Solution of Initial-Value Problems
Am. J. Comp. Math, vol. 8, pp. 7-26, 2018.
Summary: These papers outline a novel time-spectral method as an alternative to finite differencing for solution of time-dependent ordinary and partial differential equations in physics. Semi-analytical solutions in terms of Chebyshev series are obtained. The CFL condition and other grid causality conditions associated with time marching algorithms are eliminated. High efficiency and accuracy are obtained by innovative algorithms for temporal and spatial subdomains in combination with sparse matrix methods. The method is termed the
Generalized Weighted Residual Method (GWRM).

COMPUTATIONAL PHYSICS - SOLUTION OF ALGEBRAIC EQUATIONS
• Solution of Systems of Equations - a Semi-implicit Approach 
Applied Numerical Mathematics, Volume 59, Issue 10, pp. 2430-2443, 2009.
• SIR - an efficient root solver for systems of nonlinear equations
Software Quality Professional, vol. 7, s. 59-62, 2018.
Summary: The Semi-Implicit Root solver (SIR) is an iterative method for globally convergent solution of systems of nonlinear equations. SIR convergence is quasi-monotonous and approaches second order in the proximity of the real roots. Global convergence is usually superior to that of Newton's method, being a special case of the method. The algorithm
cannot land on local minima, as may be the case for Newton's method with line search.