Kurser på avancerad nivå, matematik, läsåret 2010-2011
Fall 2010
| Course code | Course name | Credit |
|---|---|---|
| SF2709 | Integration theory | 7.5 cr |
| SF2713 | Foundations of Analysis | 7.5 cr |
| SF2718 | Mathematics for Chemists | 6 cr |
| SF2720 | Chaotic dynamical systems | 7.5 cr |
| SF2721 | Topology | 7.5 cr |
| SF2723 | Topics in mathematics III: The mathematical theory of option pricing | 7.5 cr |
| SF2733 | Elementary differential geometry | 7.5 cr |
| SF2736 | Discrete mathematics | 7.5 cr |
| SF2737 | Commutative algebra and algebraic geometry | 7.5 cr |
Spring 2011
| Course code | Course name | Credit |
|---|---|---|
| SF2706 | Algebra IV | 7.5 cr |
| SF2707 | Functional analysis | 7.5 cr |
| SF2715 | Applied combinatorics | 6.0 cr |
| SF2717 | Mathematics, Advanced Course | 6 cr |
| SF2719 | The History of Mathematics | 6.0 cr |
| SF2724 | Topics in mathematics IV: Applied topology | 7.5 cr |
| SF2729 | Groups and Rings | 7.5 cr |
| SF2732 | Galois theory | 7.5 cr |
| SF2972 | Game theory | 7.5 cr |
Integration theory
KTH, SF2709, Henrik Shahgholian
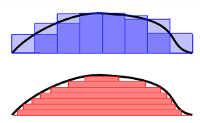
For all studies of analysis in higher mathematics it is fundamental to understand the concept of integration. Our intuitive idea of the integral of a function is as the area under its graph, and this can be turned into a formal definition through approximating Riemann sums. This leads to the Riemann integral which works fine in many circumstances, but has its limitations.
One problem with the Riemann integral is that it does not manage functions with too many discontinuities, for example the function f(x) which is 1 if x is rational and 0 if x is irrational cannot be integrated. Morally the integral should have the value zero since the rationals form a countable set which should not contribute to the integral. A more serious problem is that the Riemann integral does not behave nicely when one studies sequences of functions, such as the partial sums of a Fourier series approximating a periodic function. When can one move the limit inside the integral?
In this course we will study the Lebesgue integral, and more general concepts of integrals and measure. Among other things we will see how the above problems are resolved and we will study the important L^p spaces of functions.
The material in this course is fundamental also for the study of probability theory.
en.wikipedia.org/wiki/Lebesgue_integration
en.wikipedia.org/wiki/Measure_(mathematics)
Foundations of analysis
KTH, SF2713, Lars Svensson
Chaotic dynamical systems
KTH, SF2720, Kristian Bjerklöv/Maria Saprykina
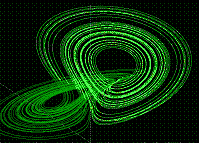
For a number of years now, chaotic dynamical systems have received a lot of scientific attention. One aspect is chaos, fractals, etc., often illustrated with the fantastic pictures -- the Mandelbrot set, Julia sets, etc. -- that computer simulations of iterations of complex polynomials give rise to.
Another aspect is formed by the so-called "strange attractors", that occur in conjunction with computer simulations of ordinary differential and difference equations. Some of the best known mathematical experiments were carried out by the meteorologist E. Lorenz and the astronomer M. Hénon, and here at the department precisely these models have been studied rigorously and chaotic behaviour was proved for them. D. Ruelle and F. Takens have proposed that turbulent phenomena might at least partially be explained via strange attractors.
The physicist M. Feigenbaum made the fundamental discovery that many systems first go through a characteristic period doubling and then behave in a random (chaotic) way, even though they are deterministic. Later, one has shown that such period doublings occur in liquid helium flow.
From a mathematical viewpoint, the course is quite special. On a relatively elementary level, one obtains insight in phenomena that lie quite close to current research. One or two computer experiments will probably be part of the course. However, the course's main emphasis will be on the mathematical theory, which in itself has a long history with names such as Poincaré, Fatou, Birkhoff, and Smale, and which lately has developed quickly, partly in symbiosis with computer experiments.
en.wikipedia.org/wiki/Chaotic_dynamical_system
Elementary differential geometry
KTH, SF2733, Jens Hoppe
Room 3733 (KTH) except the week of September 6-12, Thursdays 13-15 and Fridays 13-14. Course start: September 2

In this course we study curves and surfaces. This subject has the beauty that one can start from knowing only basic calculus, and reach many deep and interesting facts.
An important concept is that of curvature, which appears in many different forms, with the common property that it measures how much an object differs from being flat (for example an ordinary sphere has constant positive curvature, and the curvature becomes smaller as the radius is increased).
One of the important results covered in the course is the Gauss-Bonnet theorem, which relates the curvature of a surface to a topological quantity (the Euler characteristic).
Two books that will be used in the course are:
- "Differential Geometry of Curves and Surfaces" by Manfredo P.do Carmo
- "Differential Geometry:curves-surfaces-manifolds" by Wolfgang Kuehnel
Topology
SU, SF2721, Rikard Bögvad

Topology is the study of spaces from an abstract viewpoint. One is interested both in the fine structure of a space and in global features such as the number of holes. A fundamental concept is that of a continuous function, or continuous map, and the goal is to understand what properties such a map can have without using ideas like distance or derivative.
For instance, it might seem obvious that a simple closed curve in the plane divides the plane into an "inside" and an "outside" region. This observation is correct, but to really prove it assuming only that the curve is continuous is not an easy task. In fact, this was a hard problem for a long time, studied by many mathematicians in the 19th century. In the course we will see a proof of this "Jordan curve theorem", and other results such as the "Ham sandwich theorem" (one can always divide a three layer sandwich into two equal pieces with just one cut) and the "Hairy ball theorem" (one cannot comb a hedgehog).
A classical example in topology is that, in a world of perfect rubber, a coffee cup cannot be distinguished from a doughnut, but is fundamentally different from a ball. What does this observation mean? And how can one turn it into computable mathematics? The answer, perhaps surprisingly, involves group theory and abstract algebra. In the course we will see how to find and classify all two-dimensional surfaces. The doughnut and the ball are two of them.
en.wikipedia.org/wiki/Topology
Discrete mathematics
KTH, SF2736, Olof Heden
Commutative Algebra and Algebraic Geometry
KTH/SU, SF2737, Ralf Fröberg and Roy Skjelnes

Geometry and algebra might appear to be two totally unrelated subjects. The truth is, however, that affine algebraic geometry and commutative algebra are perfectly dual to each other. Grasping this duality is very satisfactory and rewarding. The main purpose of the course is to initiate the fermenting process needed to achieve this understanding.
Commutative algebra is about the structure of commutative rings. A commutative ring is a set with two operations, sum and multiplication, satisfying some natural conditions. The ring of integers and the polynomial rings are typical examples to have in mind. The notion of ideals arises when one tries to form quotients of a ring. Prime ideals are a particular class of ideals that, as the name suggests, generalize the notion of prime number.
The set of prime ideals in a ring naturally form a topological space; the spectrum of a commutative ring. The spectrum of prime ideals is a geometric object where the ideals correspond to closed subsets.
In the course we will give an introduction to these two subjects, and we will stress how to use the dictionary between algebraic geometry and commutative algebra. In particular we will focus on how algebraic notions and results are to be understood and implemented in the geometric context.
The course contains: Prime and maximal ideals, prime spectrum, Hilberts Nullstellenzats, localization and local rings, primary decomposition, integral extensions, Noetherian rings, Noether normalization.
Prerequisites: Algebra III (MM7003) or Groups and Rings (SF2729).
The course literature is Undergraduate Commutative Algebra, by Miles Reid.
Topics in mathematics III: The mathematical theory of option pricing
KTH, SF2723, Henrik Shahgholian
An option is a security/contract giving the right to buy or sell an asset subject to certain conditions, within specified period of time.
Trading option in a more organized and controlled way dates back to the founding of Chicago Board Option Exchange (CBOE) in 1973. The same year also saw a breakthrough in the theory of option pricing, with publication of the famous result of Fischer Black and Myron Scholes in the Journal of Political Economy. The mathematical model of Black-Scholes is still the most widely used tool for pricing financial derivatives.
Although uncertainty underpins the valuation of any financial instrument, the derivation of the Black-Scholes model is heavily relied on partial differential equations rather than stochastic calculus.
This model is also used for valuation of almost all financial derivatives: pricing options, pricing commodities (mines), warrants, index, ...
Since its birth, this theory has evolved to embrace very complicated phenomena beyond financial markets: Political decisions, Operating strategies, Decision under uncertainty.
In this course we shall discuss the most basic facts of this theory, using tools from PDE.
Prerequisites: Diff & Trans SF1629.
Literature:
Wilmott, Paul; Howison, Sam; Dewynne, Jeff: The mathematics of financial derivatives. A student introduction. Cambridge University Press, Cambridge, 1995. xiv+317 pp. ISBN: 0-521-49699-3, and Handouts.
Functional analysis
KTH, SF2707, Ari Laptev
The main goal is to give an introduction to the basics of functional analysis and operator theory, and to some of their (very numerous) applications.
First lecture will be on Tuesday January 18 between 14:15-16:00 in the seminar room 3721, institutionen för matematik. We continue our lectures every second Tuesday, please for more details see the course homepage.
Applied combinatorics
KTH, SF2715, Svante Linusson
Course start: Period 4
The course will cover several topics of modern combinatorics. One important question is how many are there of a certain object? We will learn techniques, such as recursions, power series and tools from algebra, to answer this question. Important objects will be permutations and partitions. We will also study some applications of graph theory, in particular flows in networks. An other interesting area is error correcting codes, where we will learn som of the basic theory. Finally we will also discuss the mathematics of voting procedures.
Prerequisite: A basic course in Discrete Mathematics. A basic course in linear algebra.
The history of mathematics
KTH, SF2719
Groups and rings
SU, SF2729, Mats Boij/Carel Faber

As James Newman once said, algebra is "a branch of mathematics in which one does something to something and then compares the results with the result of doing the same thing to something else, or something else to the same thing".
Abstract algebra is the area of mathematics that investigates algebraic structures. By defining certain operations on sets one can construct more sophisticated objects: groups, rings, fields. These operations unify and distinguish objects at the same time. Adding matrices work similarly to adding integers while matrix multiplication is quite different from multiplication modulo n. Because structures like groups or rings are richer than sets we cannot compare them using just their elements, we have to relate their operations as well. For this reason group and ring homomophisms are defined. These are functions between groups or rings that "respect" their operation. This type of function are used not only to relate these objects but also to build new ones, quotients for example.
Although at this point it may seem like the study of these new and strange objects is little more than an exercise in a mathematical fantasy world, the basic results and ideas of abstract algebra have permeated and are at the foundation of nearly every branch of mathematics.
This course is divided in two parts:
Group Theory
Rings and Modules
Galois theory
SU, SF2732, Torbjörn Tambour
Room 306, house 6, kräftriket. Thursdays 9-11. Course start: January 20

Galois theory is a beautiful and fundamental part of algebra dealing with field extensions and field automorphisms. The main theorem gives a 1-1 correspondence between the subextensions of a given field extension satisfying certain properties and the subgroups of a group of automorphisms associated to the extension.
Galois theory has many applications. Some of the best known applications are the proof of the impossibility of the trisection of a general angle with ruler and compass only and the proof that the solutions of a general algebraic equation of degree five or higher cannot be given only in terms of n-th roots and the basic algebraic operations.
Algebra IV
SU, SF2706, Sergei Merkulov
Room 306, house 6, kräftriket. Fridays 10-12. Course start: January 21
Topics in mathematics IV: Applied topology
KTH, SF2724, Wojciech Chachólski/Mattias Dahl
KTH Room 3733, Thursdays 10-12. Course start: January 20
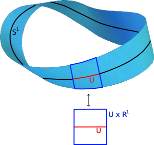
How can a topological space and its properties be described? One could try to use geometric and descriptive language. For example one might write: a 2 dimensional bounded subspace of the 3 dimensional Euclidean space without a boundary with 2 holes. Such a descriptive language however is often imprecise and may lead to wrong conclusions. For example same description could be visualize in different ways by different people. To remedy this problem, Algebraic Topology uses the precise language of algebra to describe geometry. Homology and cohomology are one of the most important tools in this translation process. It has been a great achievement in mathematics to realize that some important geometric properties of spaces can be described by these invariants. In this course we will study two specific cohomology theories: K-theory and De Rham cohomology. They both have the advantage of being elementary, and can be studied with no particular previous knowledge. K-theory deals with vector bundles over a space. An example of a vector bundle is the Möbius band which consists of a family of lines twisting around the circle. De Rham cohomology uses ideas well known from vector analysis. We will see how these theories are used to compute invariants of spaces, and we will try to give several applications.
en.wikipedia.org/wiki/Vector_bundles
en.wikipedia.org/wiki/De_Rham_cohomology
en.wikipedia.org/wiki/Algebraic_topology
Game Theory
KTH, SF2972, Jörgen Weibull, Mark Voorneveld and Jonas Sjöstrand
Game theory provides mathematical tools for the analysis of strategic interactions, with applications to many fields, ranging from political science and economics to biology and computer science. One half of this course is devoted to classical game theory and deals with "games" in a very broad sense of the word. The other half is devoted to combinatorial game theory, where we restrict our attention to a class of two-player games with perfect information, including many well-known board games like chess and go.
