Repdatorn
The Rope-and-Pulley Wonder (Scientific American, April 19, 1988)
En dator av rep block och taljor
av A. K. Dewdney
På ön Apraphul, vid Nya Guineas nordvästkust, har arkeologer upptäckt de murkna lämningarna av ett ingenjörsmässigt arrangemang med rep, block, och taljor, som man tror är den första digitala dator som någonsin konstruerats. Chefsutredare Robert L. Ripley från Charles Fort College i New York daterar konstruktionen till c:a 850 efter Kristus.
Apraphulianerna var skickliga seglare. Deras skepp var vackert byggda och utrustade med den mest utarbetade rigg man kan tänka sig. Var det så att apraphulianerna leddes till att bygga sin dator genom att de bemästrade repslagarkonsten, eller var det tvärtom? Det är en fråga som debatteras ivrigt bland experterna.
Delar av den antika block-och-talja datorn har rekonstruerats av Ripley och hans team vid "Tropical Museum of Marine Antiquities" i det närbelägna Sumatra. Gruppen har genomsökt ett område som sträcker sig flera kilometer genom tät jungel öster om Pulleg Mountains, de fann svaga spår av begravda jutefibrer och noterade de exakta positionerna för de svårt korroderade mässingsblocken och till dem hörande "hårdvara". Rekonstruktionen har gett mig ett idealiskt tillfälle att introducera läsaren i principerna för digital beräkning utan att behöva ta till små och mystiska elektroniska komponenter. Här är grindar, vippor, och kretsar, tillverkade enbart av rep, block och taljor. Allt är synligt och enkelt att förstå.
Apraphulianerna använde ett binärt talsystem precis som vi gör, men 0 och 1 representerades av repens positioner i stället för av elektriska spänningar.
Föreställ er en svart, fyrkantig, låda med ett hål borrat i en sida. Läsaren håller ett spänt rep som passerar ut genom hålet. Repets position representerar 0. Om läsaren nu drar i repet, hörs det ett klick och ett gnisslande när en replängd om en fot eller så kommer ut. Repets nya position representerar 1.
Man kan representera tal med sådana lådor. Vilket nummer som helst mellan 0 till 7 kan tillexempel representeras med 3 lådor. Genom att använda fler lådor, kan fler tal representeras. 10 lådor räcker för att representera alla tal mellan 0 och 1023.
Exemplet med svarta lådor är inte valt på måfå. Det är tydligt att apraphulianerna älskade att stänga in sina mekanismer i svarta trälådor, stora som små. Kanske var det så att konstruktion av datorn var förbehållet ett speciellt teknologiskt prästerskap. Åsynen av den stora ansamlingen av svarta lådor kan ha försatt massorna i fruktan.
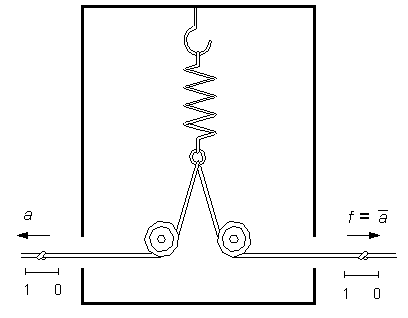
En av nyckelkomponenterna användes av Apraphulianerna för att omvandla en 0 till en 1 och en 1 till en 0. ( Det är bekvämare att använda symbolerna 0 och 1 i stället för att tala om "in" och "ut" ). Besläktad med vad moderna datoringenjörer kallar för en inverterare, består denna mekanism av en låda med ett hål borrat i lådans framsida och ett annat i lådans baksida (se figuren). När någon (eller något) drar i inmatningsrepet i lådans framsida, löper en lika stor sträcka rep ut ur hålet på baksidan. En blick in i lådan, och förklaringen är uppenbar: repet genom framsidan och ut genom baksidan passerar två block och sträcks mellan dessa mot en av kortsidorna av en ensam fjäder.
Som några läsare redan kan ha gissat, så uppfattades 0 och 1 inte så mycket av "ut" eller "in" utan mer av den riktning repet rör sig i. Detta kan bäst illustreras med en låda som saknar inre mekanism. Ett stycke rep går in i lådan genom ett ensamt hål i framsidan och vidare ut genom ett ensamt hål i baksidan. Om man drar repet från position 0 till position 1 på lådans framsida, går repet från "in" till "ut". Rörelsens riktning är mot den som drar. Samtidigt går repet från "ut" till "in" på lådans baksida, men eftersom repets rörelseriktning är mot den som drar, går även repet på lådans baksida från 0 till 1.
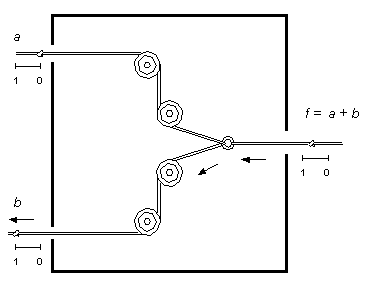
Två ytterligare mekanismer gör den antika apraphulianska repertoiren av beräknande komponenter i det närmaste komplett. Den första mekanismen hade två ingångsrep, i praktiken samma rep, som löper in i en låda. Om endera av repen var i position 1, så kom även det enda utgångsrepet att vara i position 1. Apraphulianerna löste denna funktion med förvånansvärt enkla medel (se figur). Vardera rep som löper in i lådan passerar två block som för dem nära varandra. De två repen, som löper mot lådans baksida, knöts sedan till en ensam ring som fästs i utgångsrepet. Om endera eller båda repen dras, så dras även ringen direkt. Eftersom lådans utgång blev 1 om en av ingångarna var 1, så skulle dagens ingenjörer kalla detta för en OR grind.
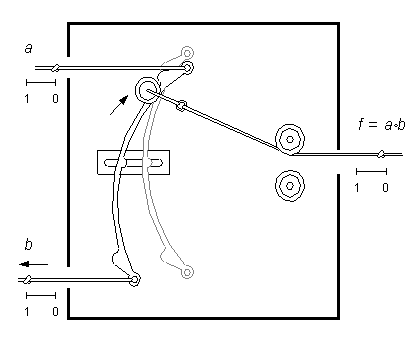
De antika Apraphulierna tillverkade vad vi skulle kalla för en AND grind av en hävarm med en löprulle och två block. Hävarmens mittpunkt var fastsatt i lådans vägg i närheten av framsidan, men den kunde löpa något i ett spår i lådans vägg. De två ingångsrepen var fastknutna i öglor i hävarmens båda ändar. Utgångsrepet utgick från hävarmens löprulle. Oavsett löprullens position på länkarmen styrdes utgångsrepet till utgångshålet med endera av de två blocken vid lådans baksida.
Om ett av ingångsrepen drogs en sträcka motsvarande 1, förflyttades länkarmens mittpunkt i spåret i riktning mot lådans framsida samtidigt som länkarmen vreds. Löprullen var fri att glida över till länkarmens motsatta ända, och därför blev förflyttningen av utgångsrepet obetydlig. Om däremot båda ingångsrepen drogs samtidigt, förflyttades länkarmen utan vridning så att hela rörelsen överfördes till utgångsrepet.
Namnet AND grind kommer av det faktum att utsignalen är 1 om och endast om ett ingångsrep och det andra ingångsrepet är i position 1.
Med dessa komponenter kan man bygga en digital dators alla styrkretsar. detta inkluderar kretsar som beräknar aritmetiska funktioner, kretsar som tolkar programkod, kretsar som styr informationsflödet mellan datorns delar.
Byggde Apraphulierna sin dator på detta sätt? Bevisen är för fragmentariska för att man ska kunna dra en slutgiltig slutsats, men arkeocomputologister som arbetar med Ripley vidhåller att de har upptäckt en enkel multiplexor bland de begravda represterna. I elektroniska datorer är multiplexorn i huvudsak en elektrisk omkopplare som dirigerar flera signaler till en enda ledning. Tillexempel har den enklaste multiplexorn två ingångsledningar som vi kan beteckna med a och b. Vid en given tidpunkt kan varje ingångsledning bära signalen 1 eller 0. Vilken av de två signalerna, a eller b, kommer att tillåtas passera igenom utrustningen och ut till en ensam utgångsledning d? Detta avgörs med en tredje ingångsledning, en kontrolledning c; om den bär på signalen 1, är det signalen från ingång a som skickas vidare genom utgångsledningen. Om, i stället, kontrolledningen är 0 är det signalen b som skickas vidare (se figur).
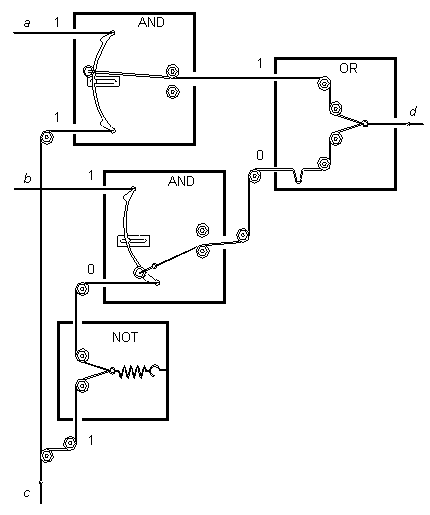
Denna rekonstruktion av en två-ingångars Apraphulin multiplexor består av två OCH grindar, en OR grind och en inverterare. Det hela är så enkelt att man vågar tro att datoramatörer kan bygga en egen Apraphulin multiplexor hemma. Järnaffärerna kanske kan komma att lida av en förbryllande brist på rep, block och taljor. I vilket fall som helst kan man följa multiplexorns funktion i figuren.
Repen a och b inkommer till multiplexorn från vänster, var och en till en egen AND grind. Repet c är splittat i två grenar. En gren leder direkt till den andra ingången i den grind som rep a är ansluten till. Den andra grenen av rep c passerar igenom en inverterare och förs därefter till den AND grind som rep b är anslutet till. Om rep c dras till ett värde 1 och hålls fast, kommer vilken sekvens av 0:or och 1:or som helst, som sänds med rep a att troget sändas den övre AND grinden och vidare till OR grinden. Samtidigt kommer en signal som sänds med rep b att stoppas vid den nedre AND grinden. Om rep c släpps till sin 0 position, kommer inverteraren att skapa 1 till den nedre AND grinden. I detta fall är det valfri signal på rep b som sänds genom den nedre AND grinden och signaler på rep a kommer att ignoreras.
OR grinden knyter bara ihop de två signalerna, så att säga. Om signalen på rep a för tillfället sänds vidare kan man enkelt se exakt vad som händer i figuren: om rep a släpps till 0 positionen, vrider sig länkarmen i den övre AND grinden och löprullen glider till ändläget. I OR grinden slackar båda ingångsrepen och utgångsrepets naturliga elasticitet drar det till den nya positionen 0. Om man drar i rep a igen, kommer förflyttningen att transporteras den beskrivna vägen, med resultatet att d sträcks igen.
Frågan om slacka rep tvingar mig att ta upp frågan om repspänningen i den Apraphuliska datorn. Ibland, som i OR grinden i exemplet ovan, kan ett rep slacka. Det finns då alltid en fara att ett sådant rep glider av ett block. Ripley har berättat för mig att Apraphulierna använde en speciell modifierad inverterare med en extremt svag fjäder för att bota problemet. När det var troligt att ett rep kunde slacka, installerade man en "svag inverterare" för att upprätthålla en minimal repspänning när signalen var 0.
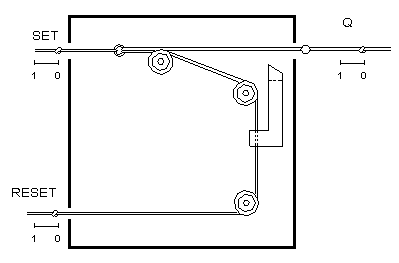
Ingen dator är komplett utan ett minne. Minnet i den Apraphulianska datorn bestod av hundratals speciella minneselement som vi skulle kalla för vippor. Återigen slås man av enkelheten i det Apraphulianska tänkandet. I enlighet med modern terminologi, betecknar vi de två repen som leder in i den mekaniska vippan med set och reset (se figur). De två repen anslöts med en serie av tre block så att när setrepet drogs ut från lådan till position 1, drogs resetrepet in i lådan till position 0. På resetrepet satt en låsarm som var rörlig längs lådans bakkant. Utgångsrepet, i praktiken en fortsättning av setrepet, hade ett stort fastklämmt sänke. När setrepet drogs och nått slutet av rörelsen hakades sänket fast mot ett spår i låsarmen. I detta läge "kommer" låskretsen "ihåg" 1.
Utgångsrepet hålls i position 1 tills den enorma repdatorn ändrar på saker och ting genom att dra i resetrepet. Detta får till följd att låsarmen dras bort från sänket och utgångsrepet intar positionen 0. Låskretsen kommer därefter att "minnas" 0. Hur användes dessa minneselement i den Apraphulianska datorn?
Ripley och hans grupp blev förbryllade när de mitt i det vidsträckta Apraphulianska datorkomplexet upptäckte ett övervuxet fält med flera tusen låskretsar av rotting placerade i rader om åtta. Ripley, med hjälp av archaeo-computologister, förmodade att fältet utgjorde den apraphuliaska datorns centrala minne. Varje rad med 8 lådor kan ha utgjort ett enstaka, åtta-bitars "ord" ("word"). På samma sätt skulle tre lådor utgjort ett tre-bitars ord, en rad med tre låskretsar som ställts in med värdena 1, 0, och 1 lagrar talet 5.
Innehållet i ett minnesord i repdatorn skulle kunnat ha hämtats på följande sätt: utgångsrepen från varje låskrets i raden leder till en tillhörande AND grind. De andra ingångsrepen till AND grindarna kommer från ett gemensamt rep som används för att hämta innehållet i det aktuella ordet. När repet dras, får AND lådornas utgångar samma värden som låskretsarna. AND lådornas utgångar leder till en stor ansamling av OR lådor och därefter till en speciell grupp med låskretsar som vi kan kalla för ett register. Ett kort ryck i repet som hör till det aktuella ordet placerar samma binära mönster av reppositioner i registret,
Datorns logiska enhet måste otvivelaktigt ha styrt informationsflödet inte bara från minne till register utan även mellan olika register. Genom användandet av mutiplexor och demultiplexor (vilket är en krets som utför den motsatta operationen), kan datorn ha sänt bitmönster från register till register. I ett speciellt register, som vi kan kalla för det aritmetiska registret, kan bitmönstren ha kombinerats enligt reglerna för addition och multiplikation.
Man tror att den Apraphulianska datorn var programmerbar. Om den var det, så användes en del av dess stora minne till att lagra program. Programinstruktionerna bestod även de av bitmönster av 1:or och 0:or som hämtades med samma mekanism som tidigare beskrivits. Dessa bitmönster sändes vid lämpligt tillfälle till ett instruktionsregister för att utvärderas av datorns logiska enhet.
Det är synd att jag inte kan göra mer på dessa sidor än att ge en glimt av den Apraphulianska maskinens stora komplexitet. Den måste ha utgjort en häpnadsväckande syn när den var i funktion. Med den enorma mängd rep som var inblandad, kan ingen mänsklig varelse ha haft styrkan att manövrera ingångsreglagen till de rätta positionerna. Närvaron av elefantskelett i det Apraphulianska området gör att kraftkällan blir uppenbar. Vid utgången upprätthöll kraftiga fjädrar tillräcklig repspänning i systemet. Kanske var det flaggor vid de yttersta utgångsrepen som möjliggjorde för det teknologiska prästerskapet att avläsa resultatet av de beräkningar som utfördes.
Den Apraphulianska rep, block och talja, -datorn utgör en intressant kontrast till dagens experiment med nanodatorer. Repdatorn tillhör förståss det förflutna, medan datorer i nanometerskala hör en osäker framtid till. Den Apraphulianska datorn var storskalig, och täckte tusentals tunnland, medan nanodatorn är otroligt liten, och rymms på en yta motsvarande en tusendel av en mänsklig cellkärna. Båda maskinerna lämpar sig som språngbräda in i den värld där spekulationer blandas med vetenskap. Tänk på de pågående drömmarna om artificiella intelligenta maskiner. Vi upplever det som enklare att acceptera möjligheten av en tänkande elektronisk dator eftersom våra tankar i stor utsträckning förmedlas genom elektriska impulser. Men eftersom varje modern dator (och dess program) i princip kan överföras till Apraphuliansk form, kommer varje artificiell dator som konstrueras i framtiden att kunna översättas till en motsvarande rep, block och talja, -dator. Kan vi föreställa oss att HAL 9000, den dator som blir paranoid i filmen 2001: A Space Odyssey, skulle kunna vara konstruerad på ett sådant sätt? Är vi villiga att medge att enorma byggnader fylla av rep, block och taljor, skulle kunna vara lika klipska som vi?
A. K. Dewdney
Visst vore det kul om detta var sant? Men artikeln dök upp i tidskriften Scientific American's aprilnummer 1988 - så det hela är naturligtvis ett välgjort aprilskämt. Visserligen fungerar alla beskrivna mekanismer, men de skulle aldrig kunna sättas ihop till en större dator - kan Du räkna ut vad som är felet?
Trots att syftet med artikeln är aprilskämtets, fungerar den ändå som en utmärkt och begriplig illustration över hur en dator fungerar. Därför har jag översatt artikeln till svenska.
A. K. Dewdney roar ofta med knepiga och tänkvärda problem i tidningen Scientific American.
Se även: En del utvecklar mekaniska logikkomponenter med hjälp av LEGO. Den första datorn var helt mekanisk Zuse Z1 1938.