På tentamenregistrering finns tre likadana tentor att registrera sig till, varför? Vilken av dem ska man anmäla sig till? En eller alla? 

Vi undersöker saken och återkommer med ett svar!

Av misstag har det blivit tre anmälningsformulär till tentan istället för ett. Det spelar ingen roll vilket formulär du använder för vi kommer slå ihop alla listor till en anmälningslista. Du behöver alltså inte anmäla dig på alla formulär utan det räcker med ett (t.ex. det första). 

Varför ser anmälan annorlunda ut, ska det vara så? Nu menar jag inte antalet, utan fältet man trycker på för att anmäla sig blir rött då man tryckt på det till skillnad från förut, då det fortsatte vara grönt. Man vill ju att tentamensanmälan ska fungera/registreras och när den ser så annorlunda ut undrar man om det ska vara så eller något är fel? 

Jag tittar på anmälningslistan och finns ditt namn med, så du är verkligen anmäld. 

Din fråga om utseendet kan jag inte svara på, men jag har skickat vidare din fråga till de som har hand om tentaanmälningar och bett dem titta på problemet.

Hej Ida!  Knappen för att anmäla sig är alltid grön, men när man har anmält sig får man en knapp så man kan avanmäla sig, och för att minska risken att folk trycker en gång till och avanmäler sig av misstag gjorde vi knappen för att avanmäla sig röd.

Hej! Har en fråga angående lösningar på vissa av uppgifterna på tidigare tentamen (ofta uppgift tre). Det står "se seminarieuppgifterna" och undrar var man kan hitta dem? //Olivia

Se denna sida.

På den sidan hittar jag bara seminarieuppgifterna men inte lösningar till dem, och därmed ingen lösning till uppgift 3 på tentan 2013-08-22. Var kan jag hitta lösningsförslag till den uppgiften?

Se lösningen till uppgift 3 på tentan 2011-10-20.

Hej! Finns det någon lösning till uppg. 3 tentamen 2013-05-27?

Se denna tråd.

Hej! Jag har en fråga på uppgift 6  2013-08-22 tentamen. Efter att jag beräknat ut Volymen och ska bestämma masscentrum till Zc så har jag problem med de rymdsfäriska gränserna, i facit står det att täta ska variera mellan 0 och pi/2, men det borde ju rimligtvis vara mellan 0 och pi eftersom att det är ett halvklot över xy-planet? Mycket konfunderad över detta och tacksam för svar. 

Jag menar det går ju inte att variera täta mellan pi/2 och 0 när man beräknar Volymen för halvklotet (visar detta matematiskt istället för att bara anta att Volymen är (4piR^3)/3*(1/2) = (2piR^3)/3, varför ska man då göra det när man beräknar masscentrum för z?

Jag är givetvis införstådd med att det är ganska stor sannolikhet att jag tänker fel. :)

Kolla igen hur rymdpolära koordinater är definierade! Det är på 33 i kursboken, eller på sidan Sfäriska koordinater på Wikipedia (observera dock att namnen på vinklarna är omkastade!)

Jag kom på att jag tänker fel, rotationen gör ju att det endast behöver gå till pi/2. Sorry. 

Tack, för tipset! Det var precis det jag behövde göra. 

Jag har en ny fråga på fråga 5 från tentamen 2013-05-27 så blir y gränserna -1 <= y <= 1, jag undrar hur dessa fås fram? Jag trodde det gick att lösa fram ur y^2 till +- sqrt(1-x) men tydligen inte. Tacksam för svar. 

Bobby:
Tror det är menat att man ska se att x är definierad i intervallet 0 <= x <= 1-y^2. Detta kräver att y ligger i intervallet -1 <= y <= 1. Om y ligger utanför detta intevall blir ju x < 0. Så har i alla fall jag tolkat uppgiften!

Aha, det har du ju rätt i, tack för inputen Hampus. Det uppskattas. :)

Vi är fyra pers som har försökt oss på uppgift 6 i tenta 2012-08-16. Vi provade Gauss' sats men fick divergensen till 0. Har vi räknat fel? Vi förstår facits lösning, men vill veta om det går att lösa med Gauss.  

Se diskussion om det elektrostatiska fältet i kursboken: Exempel 4 sid 364, och Exempel 8 sid 372!

Informera gärna när lösningsförslagen till dagens tenta är uppe :)

+1 på Max

+1 på dig kasper <3

+ 2 på båda er!

När och var kommer lösningarna upp till dagens tenta? :)

När kommer man kunna hämta ut sin tenta? 

Hej, jag är lite nyfiken på facit eller lösningsförslag till kompletteringstentan som gick 11e april nu i år om det finns nån?

Vi lägger inte upp lösningsförslag till kompletteringstentor. Du bör nu kunna se resultatet på din resultatsida, och snart ska de vara scannade.

Okej, jag var mest nyfiken på varför ett av mina svar inte stämde, hade svarat att potentialen U= x+y^2 * x^3 + C , där C är en konstant, men när jag använder U för att beräkna kurvintegralen så får jag ändå rätt för att beräkna den som U (b)-U (a)

Troligen är dom ute efter en godtycklig funktion h(x) eller h(y) istället för C.

Hej, ang. fråga 5 från tentamen 2013-01-10: Varför hittas determinanten till integrationselementet på ett annorlunda sätt än vanligt? Att det räknas d(u,v)/d(x,y) istället för d(x,y)/d(u,v) och sedan görs en reciprok på detta.. För gör man "som vanligt" fås inte 1/5dudv som det står i lösningen, utan bara 1*dudv.
Har inte sett det såhär förut men ni kanske kan hänvisa till nån sida i boken eller så?

Hej,

Vad lösningen utnyttjar är att om avbildningen (x,y) ↦ (u,v) har funktionalmatrisen A så har den inversa avbildningen (u,v) ↦ (x,y) funktionalmatrisen A^-1 (i motsvarande punkt), eller alternativt uttryckt

$$\quad\dfrac{\partial (x,y)}{\partial (u,v)} = \biggl(\dfrac{\partial (u,v)}{\partial (x,y)}\biggr)^{-1}$$

Därför kommer vi determinantreglerna ha att

$$\quad\det\dfrac{\partial (x,y)}{\partial (u,v)} = \det\biggl(\dfrac{\partial (u,v)}{\partial (x,y)}\biggr)^{-1} = \dfrac{1}{\vphantom{\Biggl(}\det\dfrac{\partial (u,v)}{\partial (x,y)}}.$$

Detta sätt att räkna ut funktionaldeterminanten genom att räkna ut "fel" determinant och invertera använder man ofta när variabelbytet är givet på formen u = u(x,y) och v = v(x,y) istället för på formen x = x(u,v) och y = y(u,v).

I uppgift 5 på tentan så är variabelbytet linjärt så det är inte så mycket extra arbete att verkligen bestämma x = x(u,v) och y = y(u,v)

$$\quad \left\{\begin{aligned}u &= x-3y\\ v &= x+2y\end{aligned}\right.\qquad\Leftrightarrow\qquad\left\{\begin{aligned}x &= \tfrac{1}{5}(2u+3v)\\ y&=\tfrac{1}{5}(-u+v)\end{aligned}\right.$$

och då är

$$\quad\det\dfrac{\partial (x,y)}{\partial (u,v)} = \det\begin{pmatrix}x'_u&x'_v\\[3pt] y'_u&y'_v\end{pmatrix} = \det\begin{pmatrix}\phantom{-}\tfrac{2}{5}&\tfrac{3}{5}\ \\[3pt] -\tfrac{1}{5}&\tfrac{1}{5}\end{pmatrix} = \tfrac{2}{5}\cdot\tfrac{1}{5}-\tfrac{3}{5}\cdot\bigl(-\tfrac{1}{5}\bigr) = \tfrac{1}{5}.$$

Därmed är

$$\quad dx\,dy = \biggl|\det\dfrac{\partial (x,y)}{\partial (u,v)}\biggr|\,du\,dv = \tfrac{1}{5}\,du\,dv.$$

Hej, jag undrar om jag som är registrerad till omtentamen den 26:e Maj ännu kan avanmäla mig och behålla mina bonuspoäng till Augusti istället?

Ja.

Hej

Vad gäller lokala undersökningar får man använda

$$f''_{xx}(a,b)\cdot f''_{yy}(a,b)-f''_{xy}(a,b)^{2}$$

som är en enklare variant av den kvadratiska formen. Får jobbet gjort bra mycket snabbare än \(Q(h,k)\). Är den för bekväm eller varför nämns den öht inte i kursen?

Tenta 2013-01-10 igen..fråga 8. Varför antas det att punkterna (+-1,+-2) ligger på ellipsen? Är det nåt man kan läsa ur rektangelns koordinater (känner inte igen sättet att skriva på, med hakparentes).

Hej Amadou,

Det handlar inte om att lösa uppgiften så snabbt som möjligt. Det är inte därför vi vill att du löser uppgifter. När du löser en uppgift så tycker jag att du ska använda en metod som gör att du verkligen förstår varför du får fram det svar du får, istället för att bara använda en färdigt formel som du lärt dig utantill och egentligen inte förstår något av.

Många gånger är det bättre för ens förståelse att ta flera steg tillbaka och härleda resultat. Det tar visserligen längre tid i början, men det är tid som man tjänar igen senare och gör att man enklare kan gå vidare till saker som bygger på detta. Det är först när man verkligen förstått en sak som man kan börja med att tänka på att göra saker på ett snabbare sätt.

I ditt exempel skulle jag vilja gå tillbaka och utgå från Taylors formel. Säg att du har den stationära punkten (x,y) = (1,1) till funktionen f(x,y) = x³ + y³ - 3xy och vill undersöka om punkten är ett lokalt max, min eller ingetdera.  Då börjar vi med att Taylorutveckla funktionen kring (x,y) = (1,1) eftersom Taylors formel talar om hur funktionen ser ut lokalt kring den punkten,

$$\begin{aligned} f(1+h,1+k) &= f(1,1) + \tfrac{1}{2}\bigl[f''_{xx}(1,1)h^2+2f''_{xy}(1,1)hk + f''_ {yy}(1,1)k^2\bigr] + \text{restterm}\\ &=-1 + \tfrac{1}{2}\bigl[6h^2-6hk+6k^2\bigr] + \text{restterm}\\ &= -1 + 3(h^2-hk+k^2)+\text{restterm.}\end{aligned}$$

Detta säger oss att i punkter (x,y) = (1+h,1+k), där h och k är små, så har funktionen väsentligen utseendet f(1+h,1+k) ≈ -1 + 3(h²-hk+k²), dvs de dominerande termerna är 3(h²-hk+k²). Vi skriver nu om dessa termer med kvadratkomplettering till

$$\quad 3(h^2-hk+k^2) = 3\bigl((h-\tfrac{1}{2}k)^2-(\tfrac{1}{2}k)^2+k^2\bigr) = 3\bigl((h-\tfrac{1}{2}k)^2+\tfrac{3}{4}k^2\bigr).$$

Nu ser vi de dominerande termerna är positiva när (h,k) ≠ (0,0). Detta betyder att så fort (x,y) = (1+h,1+k) avviker från (1,1) så kommer funktionsvärdet f(1+h,1+k) att få ett positivt bidrag från de dominerande termerna och därmed vara större än f(1,1). Funktionen måste alltså ha en lokal minimipunkt i (x,y) = (1,1).

Jämför ovanstående resonemang med harangen "Eftersom \(f''_{xx}(1,1)=6>0\) och \(f''_{xx}(1,1)f''_{yy}(1,1)-(f''_{xy}(1,1))^2 = 6\cdot 6-(-3)^2 = 27 > 0\) är punkten (x,y) = (1,1) en lokal minimipunkt". Detta är ingen förklaring av varför det är en lokal minipunkt utan bara en utantill-kunskap (och vad gör du om du glömt bort om det ska vara > 0 eller < 0?). 

Din minnesregel (som också kallas för abc-testet) fungerar dessutom bara när du har en funktion av två variabler. Metoden med att Taylorutveckla och undersöka den kvadratiska formen med kvadratkomplettering fungerar däremot även för funktioner av tre, fyra, ... variabler.

Hej

Jo jag vet att det är "dum"-alternativet till den kvadratiska formen (kanske därför amerikansk litteratur flitigt använder den hehe). Naturligtvis måste man förstå vad man gör jag undrade bara då den påminde mig om andraderivatatestet i envariabelanalys, ett enklare test än teckenstudium.

Hej Hermina,

Skrivsättet [-1,1]×[-2,2] betyder -1 ≤ x ≤ 1, -2 ≤ y ≤ 2 och rektangelns hörnpunkter är därför (±1,±2), så vad som sägs är att ellipsen måste gå genom rektangelns hörnpunkten.

Det går att komma fram till detta genom att först konstatera att ellipsen är spegelsymmetrisk i både x- och y-axeln så om en hörnpunkt ligger på ellipsen, t.ex. (1,2), så kommer alla fyra hörnpunkter automatiskt ligga på ellipsen. Frågan kan därför kokas ned till: Varför ligger hörnpunkten (1,2) på ellipsen?

Jo, antag att (1,2) inte ligger på ellipsen. Då ligger ellipsen utanför (1,2) (eftersom ellipsen ska ju innehålla hela rektangeln). I denna situation går det att minska på en av ellipsens halvaxlar så att den fortfarande innehåller hela rektangeln men har mindre area. Det går att minska halvaxeln tills ellipsen slår i hörnpunkten (1,2). Se figuren.

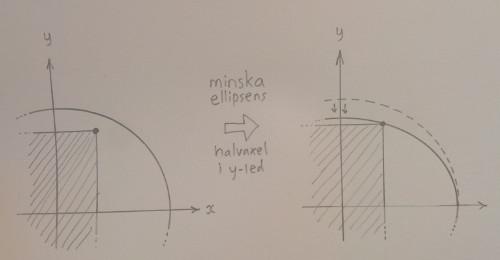
Man kan alltså utgå från att den sökta ellipsen (som har minst area) är en ellips som innehåller rektangelns hörnpunkter.

Tack Tommy för svaret - hade inte ens tänkt tanken att klamrarna var "villkorsklamrar" :-)

Hejsan Tommy jag undrar lite angående tentan bedömningskriterierna ovan vad anser ni är ett mindre räknefel? :)

Hej,

Det är förstås en omöjlig fråga att besvara i allmänhet. Den meningen som står i texten fångar nog trots allt andemeningen på ett bra sätt om vad vi anser vara ett mindre räknefel.

Hej, får bonuspoäng tas med till plussning?

Ja, bonuspoängen gäller även vid plussning.

Vem gör tentan den 21 augusti?

Examinator är Mattias Dahl.

Se denna tråd.

Hej!

Då elevexpeditionen har sommarstängt undrar jag hur man går tillväga för att anmäla sig för att plussa flervarren vid augustitentan (man kan ju inte anmäla sig på nätet då).

Tacksam för svar! :)

Hej,  skicka ett mail till mig (tek@kth.se) så lägger jag in din ansökan nästa gång jag är på KTH.

Här fanns en lite rörig och missvisande diskussion om seminarieuppgifterna. För att inte skapa onödig förvirring så har jag dolt den.

All information om seminarieuppgifterna finns på sidan Allmänt om seminarierna.

Seminarieuppgifterna kommer från boken och finns i fliken kursinnehåll.

Övningsboken alltså.

vart kan man hitta semenarie uppgifter?

Kan någon förklara om gruppindelning? Jag vet inte om jag tillhör nån grupp eller inte och vart kan man hittar detta? Och även seminarie upgifterna?!

MVH

Om du går in på din resultatsida så hittar du information om i vilken seminariegrupp du tillhör. Seminarieuppgifterna hittar du under kursinnehåll och allmän information om seminarierna under allmänt om seminarierna.

Tack Tommy!

MVH

Hej, en fråga inför omtentan... Hör bonuspoängen till enbart del A på tentan? 

Mvh Nadja

Ja, dina bonuspoäng adderas till den poängsumma du får på del A. Du kan dock maximalt få 12 poäng på del A.

Hur får man redapå vilken seminarie grupp man tillhör ?

Nyss skickade vi ut epost-meddelanden till alla med information om seminariegruppen. Den informationen finns också under länken "Seminariegrupper" på din kursomgångssida (se högerspalten i den ruta som gäller för ditt program).

Var hittar jag lösningarna till seminarieuppgifterna? Många tentor  hänvisar till lösningarna till seminarieuppgifterna.

Tyvärr finns inga lösningar, men ställ gärna en fråga om du har problem med något av problemen.

Hej!

Skulle vilja veta svaret till uppgift e från seminarium 4? :)

Tack så mycket på förhand!

Mvh,

Yuwei

Ingen av uppgifterna på seminarium 4 har en e-uppgift. Vilken uppgift menar du egentligen?

Oj, fel - jag menade uppgift 3 :)

Se tentamen 2011-10-20 uppgift 3.

Kontrollskrivningar finns inte, men vissa seminarier är som kontrollskrivningar, läs under Allmänt om seminarierna.

Fråga: om ordinarie tentamen gick i Mars, 2014, räknas bonuspoängen på första omtentamen i Augusti 2014?

Bonuspoängen för detta läsår gäller även i augustiperioden, men det är sista tentatillfället de gäller.

Finns det inga seminarieuppgifter för Kapitel 3 som är rekommenderade för skrivningen? Tack på förhand!

Hur vet man vilken utav de tre tentorna som finns uppe man ska anmäla sig till? Ingen sådan specifik information har väl gått ut?

Av misstag har det blivit tre anmälningsformulär till tentan istället för ett. Det spelar ingen roll vilket formulär du använder för vi kommer slå ihop alla listor till en anmälningslista. Du behöver alltså inte anmäla dig på alla formulär utan det räcker med ett (t.ex. det första).

Tommy: Den kursplanering som vi fick ut i samband med kursstart skiljer sig lite från denna när det gäller vilka seminarieuppgifter man ska göra till olika seminarier. Bl.a står det i vår kursplan att uppgift 9.2 ska göras till seminarie 5 medan här står det att den ska göras till seminarie 6. Vad är det som gäller?, d.v.s. vilka uppgifter är till vilka seminarier?

Kursomgången för CDEPR och CMATD har de två sista seminarierna omkastade, så för oss gäller att seminarium 5 handlar om kurvintegraler och seminarium 6 om area- och trippelintegraler.

Hur är det med upg 8.15? Den är på weben markerad som sem.6 vilket då borde bli omkastat till sem.5? men pappren från föreläsningarna är den inte med på sem 5?

Den är lagd under seminarium 6 eftersom vi går igenom areaintegraler samma dag som seminarium 5 går.

Hej, jag har en fråga. Jag läser om kursen och även om jag läser kursen med en omgång exempelvis CMETE1 så får jag bara gå på de här seminarierna? Och inte CMETE1s seminarietillfälle? 

Jag antar det, annars skulle de ju inte skapa speciella seminarietillfällen för omregistrerade. Det var så på kursen sf1624 när jag läste den i höstas i alla fall.

Ok, förr har man alltid varit med på samma seminarier som den omgång man läste med nämligen...

Hur fungerar det med seminarieuppgifterna då man har olika upplagor av övningsboken? 

Det är senaste upplagan som gäller. Om du har en äldre upplaga får du jämföra med en kompis.

Vänliga hälsningar, Mattias Dahl

Hej!

Det kanske skulle vara bra om det sattes in en extra sal och en extra assistent med tanke på hur många det var som kom på seminariumet. Det var en omöjlighet att få plats om man hade föreläsning i kursen 15-17 och sen seminarium 17-19. Det var nämligen fullt i alla salar redan 16.30 vilket skapar en minst sagt ohållbar situation för de flesta av oss som måste läsa kursen igen. 

Mvh Bobby

Vi försöker ordna fler seminariesalar om det går. Information kommer!

Toppen! Och tack, för snabbt svar. :)

Nu finns en extra grupp, se Grupp 4 här ovanför!

Jag missade seminarie ett, och är omregistrerad, kan jag komplettera det i efterhand? Dessutom undrar jag om det finns plats kvar i någon grupp? Grupp 4 skulle passa mig bäst!

Se sidan med svar på Vanliga frågor

Hej! Jag kommer inte kunna gå på seminarie 6 med min ordinarie grupp 2 då jag har förhinder på måndagen.(3/3) Kan jag gå onsdagen istället? Måste jag säga till det till någon?

Hej,  Jag har svarat via epost.

Hej!

Jag ska gå på seminarierna för omregistrerade nu i period 4 men jag har samma problem som ovan, jag kommer inte kunna gå på seminarie 3 med min ordinarie grupp (förhoppningsvis 4) p.g.a. krock. Kan jag gå på tisdagens tillfälle då? 

Hej,

Du kan gå på tisdagens seminarium 3 i mån av plats, men du är inte garanterad en plats annat än i din ordinarie grupp.

Hej,

Undrar om det är just denna bok som ska användas till flervariabelanalys eller duger det med den också : Flervariabelanalys med linjär algebra av Torbjörn Kolsrud ?!

MVH

Waheed

20/10 -11 tentan upg. 5 Vad händer med jacobianen när bytet till polära koordinater görs?

Det görs aldrig något byte till polära koordinater utan r är en konstant (cylinderns radie)

Kommer ni lägga upp lösningsförslag på kompletteringstentan?

Nej, vi brukar varken lägga upp kompletteringstentor eller lösningar. Den kommer dock bli rättad ganska snabbt så du får resultatet inom några dagar (och kan då hämta ut den på expeditionen).

Skriver du här eller så när ni rättat de?

Visst.

Anmälan till tentamen 19 oktober

Sista anmälningsdag för tentamen den 19 oktober är söndagen den 30 september kl 24.00. Anmälan görs på Mina sidor.

Den som vill tentera upp sitt betyg (s.k. plussare) ska anmäla sig på matematiks studentexpedition denna vecka.

Nu är placeringen för tentamen den 19 oktober, 8:00-13:00 färdig. På din personliga resultatsida kan du se i vilken sal du ska skriva.

Kom ihåg att ta med fotolegitimation. För att få skriva tentamen får du inte komma senare än 45 minuter efter skrivtidens början.

För de som missat att anmäla sig finns ca 5 reservplatser i salen F1. Det är "först till kvarn" som gäller för dessa platser. Efter 45 minuter kan man även ta outnyttjade platser.

Anmälan till tentamen 10 januari

Sista anmälningsdag för tentamen den 10 januari är söndagen den 16 december kl 24.00. Anmälan görs på Mina sidor.

Den som vill tentera upp sitt betyg (s.k. plussare) ska anmäla sig på matematiks studentexpedition denna vecka.

Nu är placeringen för tentamen torsdagen den 10:e januari, 8:00–13:00 färdig. På din personliga resultatsida kan du se i vilken sal du ska skriva.

Kom ihåg att ta med fotolegitimation. För att få skriva tentamen får du inte komma senare än 45 minuter efter skrivtidens början.

För dem som missat att anmäla sig finns 17 reservplatser i salen Q1. Det är "först till kvarn" som gäller för dessa platser (ingen anmälan). Efter 45 minuter kan man även ta outnyttjade platser.

Hej! För oss "plussare" till tentan den 10e: var kommer vi att skriva och hur/när får vi veta detta?

Gå in på din personliga resultatsida. Där står var du ska sitta.

Har examination även gjort en modtenta, eller är det bara oktobertentan som går att kika på?

Det finns ingen modelltenta utan det är tentorna sedan 2011-10-20 som är mest relevanta. (Kursen har inte förändrats sedan förra läsåret.)

Om det är så att man är anmäld att plussa tentan, men väljer att inte skriva den - måste detta föranmälas på något sätt?

Nej, du behöver inte göra något.

Lösningarna till dagens tentamen är nu upplagda på denna sida.

Tyvärr är vi lite underbemannade i rättningen av tentan så det kommer ta minst en vecka innan den är rättad.

Tentamen 10 januari rättad

Gå till denna sida för att se ditt resultat. Statistik finns på denna sida.

Tentorna finns för uthämtning i mattes studentexpedition imorgon och resultaten kommer bokföras i ladok troligtvis under nästa vecka. De som fick betyg FX kommer få information om kompletteringstentan via epost.

ungefär när kommer mail om kompletteringstentamen att skickas ut?

Med all sannolikhet nästa vecka.

Hej. Finns det något annat tillfälle mellan 12e mars och 27e maj där man kan skriva en flervariabelstenta? Vare sig det är ett omtenta tillfälle eller ordinarie tentamen?

Med vänlig hälsning, Mary

Nej, de återstående tentorna detta läsår går i mars, maj och augusti

Anmälan till tentamen 12 mars

Sista anmälningsdag för tentamen den 12 mars är söndagen den 24 februari kl 24.00. Anmälan görs på Mina sidor. Det är många anmälda (just nu 785 st) och därför är det extra viktigt att anmäla sig eftersom det troligtvis inte blir många reservplatser.

Den som vill tentera upp sitt betyg (s.k. plussare) ska anmäla sig på matematiks studentexpedition denna vecka.

Hej!Jag upptäckte i onsdags att jag inte var kursregistrerad och kan inte anmäla mig till tentan (jag har däremot kunnat anmäla mig till KSar och gå på seminarier) och har försökt ringa till matematikexpeditionen varje dag sedan dess men aldrig kommit fram. Går detta att fixa innan imorgon? Om inte, kan jag försöka på måndag igen och kanske säkra en plats ändå?

mvh Astrid

Jag har lagt ett meddelande till kurssekreteraren om att du vill bli registrerad och delta på tentan. Såvida det inte är något problem med att registrera dig så finns goda förhoppningar att du får en plats på tentan. (Annars kan du gå till eventuella reservsalar.)

Tack så mycket för hjälpen!

Hej

Märkte precis också att jag inte var kursanmäld och därmed inte sett tenta anmälan..

Går de att ordna ?

Mvh Sixten

Jag har skickat din förfrågan till kurssekreteraren som har hand om salsplaceringen. Om du har tur så går det, annars får du skriva i eventuell reservsal.

Jag kontaktade Kerstin med hon säger att jag måste göra ett kursval, vad det nu innebär, så jag är fortfarande inte registrerad på SF1626 och kunde därmed inte anmäla mig på tentanem den 12 mars. Vad gör man nu?

Prata med din studievägledare så får du hjälp.

Jag har en fråga angående lösningsförslaget till tenta 2013-01-10
Både fråga 4 och 5 innehåller momentet att räkna ut determinanten till en Jakobimatris (integrationselement). I fråga 5 tar man J\(\exp -1\), men i fråga 4 nöjer man sig endast med J. Vad kommer detta av?

I de två uppgifterna görs variabelbytet åt olika håll: I Uppgift 4 har vi uttryck för \(x, y\) som funktioner av de nya variablerna \(r, \varphi\), i uppgift 5 har vi de uttryck för de nya variablerna \(u, v\) som funktioner av \(x, y\).

Tack!
Då undrar jag en annan sak ang. fråga 5 på tenta 2012-06-04
När man ska beräkna dubbelintegralen, borde man inte då kunna parametrisera områder D:
x = cos(t)
y = 1 + sin(t) , där t varierar mellan 0 och 2 pi
Svaret får jag då till 22 pi (och inte 11 pi). Varför?

Om du skriver din parametrisering som

$$\quad (x,y) = (0,1) + (\cos t,\sin t)$$

så kanske du lättare ser att det du gör är att du parametriserar cirkeln med medelpunkt i (0,1) och radie 1, dvs randcirkeln till området D.

För att du ska parametrisera hela cirkelskivan D så behöver du även variera radien med en parameter r, dvs

$$\quad (x,y) = (0,1) + (r\cos t, r\sin t)$$

där r och t är parametrar; r går mellan 0 och 1, och t går mellan 0 och 2π.

En tumregel är att man behöver en parameter för att parametrisera ett en-dimensionellt objekt (t.ex. en cirkel) och två parametrar för att parametrisera ett två-dimensionellt objekt (t.ex. en cirkelskiva).

Hej! Jag har ett problem med att bestämma integrationsgränser. Till exempel ten uppgift 2 2011-10-20. Delområde 2: x ligger mellan 1 och 2 och för y har man den undre gränsen -x och den övre gränsen -3x+4, jag förstår att det ska vara -x och -3x men hur kan man se eller beräkna +4? Säkert inget svårt men jag får bara inte till det.

Den övre gränsen är den räta linje som går genom punkterna (1,1) och (2,-2). Om vi skriver den linjen som y = kx+m så får vi fram ett ekvationssystem för k och m genom att stoppa in punkterna (1,1) och (2,-2),

$$\quad\begin{aligned}1 &= k\cdot 1 + m\\ -2 &= k\cdot 2+m\end{aligned}$$

Detta system har lösningen k = -3 och m = 4. Därför är y = -3x + 4.

Jahaa! Åh vad bra att det var så man skulle göra, hade passerat mig helt. Tack!

Hej på fråga sex från tentan  20120816 får jag svaret \(4\Pi /R\) och jag använder mig av den hårda vägen genom att först skriva F som funktion av lambda och theta och sedan . Då får jag som lösningen visar 

$$m=F(r(\lambda ,\theta))=1/R^3(1,1,1)$$

Rymdpolära koordinaterna x,y,z

$$(r(\lambda ,\theta))=(Rcos(\lambda)sin(\theta ),Rsin(\lambda)sin(\theta),Rcos(\theta)$$

Sedan partialbråksuppdelar jag och med avseende på theta först och sedan lamda och kryssar dem i den ordningen och får då \(N=(r(\lambda ,\theta))Rsin(\theta))\)

Efter det så tar jag och löser integralen\(\iint_{D}m\cdot N d\theta d\lambda\) över område d där theta går mellan o och pi och lamda mellan 0 och två pi.

$$\iint_{D}m\cdot N d\theta d\lambda= 1/(R\exp3) R\exp 2 \iint_{D}m\cdot N d\theta d\lambda= 4\Pi /R$$

Vart gör jag fel?

Du missar ett R. Om vi använder dina beteckningar så är

$$\quad \overline{m} = \dfrac{1}{R^3} (r(\lambda,\theta))$$

och det ger sedan att

$$\quad \overline{m}\cdot\overline{N} = \dfrac{1}{R^3}\,R\sin\theta\:\overline{r}(\lambda,\theta)\cdot\overline{r}(\lambda,\theta) = \dfrac{1}{R^3}\,R\sin\theta\:R^2 = \sin \theta$$

som du därefter integrerar över 0 ≤ θ ≤ π, 0 ≤ λ ≤ 2π och det ger 4π.

Ställer en följdfråga på uppg 6 från tentan 2012-03-12 Skall man bestämma potentialen på \(\frac{E=k(x,y,z)}{(x^2+y^2+z^2)^(3/2)}\) betyder det att man ska tolka att det står till detta \(E=\left[x,y,z \right]=\frac{k}{x^2+y^2+z^2)^(3/2},\frac{k}{x^2+y^2+z^2)^(3/2},\frac{k}{x^2+y^2+z^2)^(3/2}\)

Eller skall man tolka det som att de står till

$$E=\left[x,y,z \right]=\frac{kx}{x^2+y^2+z^2)^(3/2)},\frac{ky}{x^2+y^2+z^2)^(3/2)},\frac{kz}{x^2+y^2+z^2)^(3/2)}$$

Det är den sista tolkningen som är rätt.

Hej! 

Vem ska jag meddela att jag har dyslexi och har rätt till 50% längre skriv tid på tentamen ?

Se denna sida

Jag har redan ett intyg från KTH grejen är att jag vill ha 50% extra tid på tentan i flervariabeln nu den 27 maj hur löser ni det?

Om du har ett intyg från Funka på att du ska ha 50% extra skrivtid så är det redan inlagt i systemet och vi får sedan den informationen när anmälningslistorna laddas ned. (Jag kan faktiskt redan nu se i anmälningslistan att du ska ha extra skrivtid, så informationen finns där.)

Hur ser taylors formel ut när man räknar ut taylorpolynomet av grad 1 med 2 variabler?

Taylorutveckling av funktionen f(x,y) kring punkten (a,b):

$$\quad f(a+h,b+k) = f(a,b) + f'_x(a,b)h + f'_y(a,b)k + \text{restterm.}$$

Där resttermen har utseendet

$$\quad \text {restterm} = |(h,k)|\,B(h,k) = \sqrt{h^2+k^2}\,B(h,k)$$

och B(h,k) är en begränsad funktion i en omgivning av (h,k) = (0,0).

Hej igen! Ang tenta 2013-03-12. a uppgiften

Varför kan man sätta detta villkor?

h, k < 0

MVH Michaéla

Det är bara riktningar (h,k) utifrån punkten (1,1) som pekar in i kvadraten D som ska undersökas. Om du tittar på bilden i lösningen så ser du att (h,k) ska befinna sig i tredje kvadranten av hk-planet, dvs att h ≤ 0 och k ≤ 0.

Hej! 

På uppgift 4b på tentan från 2013-03-12 kan man istället för att hitta potetialen räkna som om det vore en "vanlig" flödesintegral och parameterisera funktionen? 

MVH Taylor 

Ok, men jag förstår faktiskt inte varför de hamnar i tredje kvadranten. v pekar väl inåt i alla kvadranter?

Tack för svar!

@Taylor: Ja, du kan välja en kurva och beräkna kurvintegralen via parametrisering.

@Michaéla: I bilden nedan har jag ritat in fyra vektorer (h,k) som pekar i fyra olika riktningar:

• Vektorn v₁ = (h,k) har h < 0 och k < 0.
• Vektorn v₂ = (h,k) har h < 0 och k > 0.
• Vektorn v₃ = (h,k) har h > 0 och k > 0.
• Vektorn v₄ = (h,k) har h > 0 och k < 0.

Från bilden framgår att för att v = (h,k) ska peka in i D så måste h ≤ 0 och k ≤ 0 (dvs fall 1 ovan).

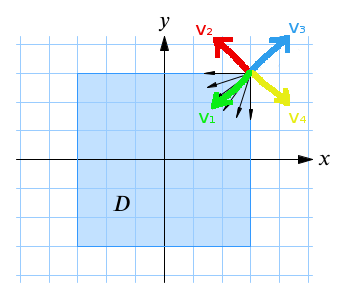
Hej!

I lösningsförslaget till uppg 1A i ten 2012-06-04 så får ni gradg(2,1,-1)=(-1,-2,4). Jag får z till minus 4, dvs =(-1,-2,-4).

Har jag räknat fel lr?

Får du samma ∂g/∂z som lösningsförslaget?

nej, och jag hitta ett fel jag gjort. Tack!

Tack för bra förklaring!

Hejsan igen! Nu har jag en till fråga.. på tentamen 2012-19-20 uppg 9 så fås y av roten ur(1-z2-x2). Det jag undrar är varför utesluts den negativa roten? I uppgiften anvöns enbart y = den positiva roten!

Tack för svar

I uppgiftstexten står det att y ≥ 0.

Hej! Jag undrar hur man får fram enhetsnormalen som behövs när man ska bestämma flödet av fältet i uppgift 5, tentamen 2011-10-20. 

Tack för svar! 

Se detta inlägg.

Taylors formel för tre variabler kan du till exempel se här (se sid 3):

http://ingforum.haninge.kth.se/armin/ALLA_KURSER/SF1626/TAYLOR.pdf

Formelsamling är inte tillåten på tentan.

Fråga 9, tenta 2013-03-12, varför optimerar man på enhetscirkeln?

Fråga 8 på tentamen 2013-01-10: Hur ser rektangeln egentligen ut? Eftersom rektangeln ska vara [-1,1]x[-2,2] blir den ju noll...

@Annie: Punkten (x,y) är fix och lika med (1,1). I den punkten optimerar du \(f'_{\boldsymbol{v}}(1,1)\) över alla enhetsvektorer v = (h,k) som pekar in i D (dvs h ≤ 0 och k ≤ 0) och om (h,k) ska vara en enhetsvektor måste h² + k² = 1. Det är därför du får en enhetscirkel att optimera över.

@Rebecca: [-1,1]×[-2,1] betyder rektangeln där -1 ≤ x ≤ 1 och -2 ≤ y ≤ 2.

Hej!

Jag kan inte hitta vilka salar som är reservsalar för tentamen imorgon den 27e maj. Är det någon som vet vilka salar som gäller?

En fråga i sista minuten, förstår om ni inte svarar!

2013-03-12, uppgift 8. När variabelbytet utförs och detatminanten bli -1\2, varför tas minus tecknet bort?

Mvh Michaéla 

Det kan jag svara på Michaela!

När man gör variabelbyte så ersätts dxdy = |J|dudv, det vill säga absolutbeloppet av determinanten! Alltså blir det |-1/2| = 1/2

Tack så hemskt mycket!

tentamen 27/5 - 2013. upg 4b. hur får man fram pi/6 som ska vara vinkeln till punkten (0,1,sqrt(3))

Om du tittar på rz-planet där 'r' är avståndet till z-axeln, vill du ha vinkeln 'θ' mellan vektorn '(1,sqrt(3))' och z-axeln. Eftersom vektorns längd är '2' får vi att 'sin(θ)=1/2' eller 'cos(θ)=sqrt(3)/2' och därmed 'θ=π/6'.

Använd sen en annan variabel för beteckning av avståndet till origo :) t.ex. 'R'.

Hej Fredrik!

Vinkeln \(\theta\) går mellan z-axeln och vektorn ut till den aktuella punkten. I den här uppgiften är \(\theta\) alltså vinkeln mellan z-axeln och vektorn från origo till (0,1,sqrt(3)).

Eftersom vi inte rör oss alls i x-planet (alla koordinater 0), kan vi studera bara yz-planet. Tänk dig den rätvinkliga triangel som går mellan origo, (0, 1, sqrt(3)) och (0,0,sqrt(3)). Den räta vinkeln ligger alltså vid punkten (0,0,sqrt(3)). \(\theta\) kan man nu få fram genom att beräkna till exempel tan \(\theta\) = 1/sqrt(3). Inom det möjliga intervallet för \(\theta\), uppfylls detta av \(\theta = \pi/6\).

/Rebecca

Hej! 

Har lite problem med att förstå hur man tar fram en potential till ett vektor fält.

skulle någon kunna förklara? 

Låt

vi söker då en potential 'U(x,y,z)' där

alltså

.

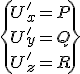Vi integrerar upp ovanstående uttryck och får

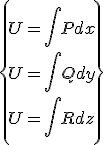
därefter löser vi systemet och får en potential 'U'.

Uppgift 9.29

Vi söker då en potential 'U(x,y)' där

.

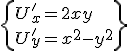Sedan integrerar vi upp uttrycket och får

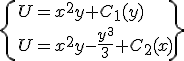
detta ger att

där 'C' är en konstant.

Hej, Fredrik!

Jag tar tre dimensioner, två fungerar likadant.

Vi har vektorfältet F(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z)), och vill hita en funktion U sådan att:

$$\left\{ \begin{matrix} \frac{\partial U}{\partial x} = P \\ \frac{\partial U}{\partial y} = Q \\ \frac{\partial U}{\partial z} = R\end{matrix} \right.$$

Var och en av dessa ekvationer kan integreras, så att man får:

$$\left\{ \begin{matrix} U(x, y, z) = \int P(x, y, z)dx \\ U(x, y, z) = \int Q(x, y, z) dy \\ U(x, y, z) = \int R(x, y, z)dz \end{matrix} \right.$$

det vill säga primitiva funktioner till P, Q respektive R, med avseende på var sin variabel.

Det man gör är då att man väljer ut vilken av de tre integralerna som ser lättast ut att utföra, till exempel den första, och utför den. Då får man att \(U(x, y, z) = \int P(x, y, z) dx = \hat P (x, y, z) + g(y, z)\)

Där är \(\hat P\) en primitiv till P med avseende på x. g(y, z) är där av samma anledning som man får en integrationskonstant när man tar fram endimensionella primitiver: Den kan vara vad som helst, eftersom den ändå försvinner när man deriverar m.a.p. x. Med ett konkret exempel kommer alltså \(\hat P\) vara något konkret uttryck av x, y och z, medan funktionen g fortfarande är okänd, och man skriver helt enkelt g(y, z).

Nästa steg tycker jag är att derivera U med avseende på y och z, och jämföra med Q och R. Man får då med den okända termen \(g'_y(y, z)\) respektive

... respektive \(g'_z(y, z)\) i de båda uttrycken. Går det att välja g på ett sådant sätt att U:s derivator blir rätt?

Om man hittar ett sådant g (ibland funkar 0, hurra!), har man hittat en potential. Om man lyckas visa att det inte går, har man bevisat att det inte finns någon potential.

/Rebecca

Hej jag har en fråga angående facit till tentamen 2013-08-22. På fråga 7 beskrivs triangelns område som x=-1, 0=< y =<z och 0=<z=<2. Jag försöker rita upp det området men kommer fram till att det område istället beskriver en triangel med hörnen i (-1,0,0), (-1,0,2) och (-1,2,2), Borde inte olikheten till triangeln i fråga vara x=-1, z=<y=<2 och 0=<z=<2?

Jo, du har rätt, det var ett fel tidigare! Om du laddar ner lösningarna igen ser du den nya (förhoppningsvis korrekta) versionen.

Hej ! Jag ara undrar när nästa tenta tillfälle är 

Under läsåret 13-14 ges denna kurs i perioderna 3 och 4. Tentor kommer i slutet av dessa perioder.

Hej! Jag har en fråga angående kompletteringstentamen. I mailet som man fick så står det att uppgifterna på kompletteringen kommer vara utav samma karaktär som B-uppgifterna på tentamen, innebär det att det kommer vara samma "typ" av tal som tal 4,5,6 på tentan 13-08-22? Dvs en minsta - största värde, taylor och sfärisk volym?

Tack på förhand

Nej, det betyder inte att frågorna handlar om samma sak som på tentan. Vad som avses är att frågorna är av ungefär samma svårighetsgrad och omfattning som B-uppgifterna.

Man kan ju alltid hoppas! Men då vet jag det, tack för snabbt svar!

Hej jag tror inte jag är kursregistrerad då jag inte kan anmäla mig till kontroll skrivningen

Anmälningsformuläret till KS1 aktiveras först imorgon (22 mars), men du har rätt i att du inte var registrerad. Jag har bett kursadministratören registrera dig.

Hej, jag har heller inte blivit kursregistrerar och kan således inte anmäla mig till KS1 som öppnar imorn

Hej, jag har inte heller blivit registrerad på kursen...

@Erik och @Johannes: Kursadministratören har nu fått i uppdrag att kursregistrera er.

Hej, jag är inte heller registrerad på kursen än. Tänkte gå kursen med Open om det gör någon skillnad för registrering, kommer från datateknik som inte går den längre.

David, du är redan registrerad på kursen.

Hej! Jag tror inte att jag är kursregistrerad

Hej, jag behöver bli kursregistrerad.

@Sebastian & @Luciano: Ivägskickat till kursadministratören och hon återkopplar när ni är registrerade (troligtvis på måndag).

Hej jag vill också bli kursregistrerad, och gärna tillsammans med CKEMV och CBIOT-programmen. Jag skickade ett mail till Anne Riddarström men har inte fått något svar.

Rikard Israelsson

Jag påminner Anne på måndag.

Hej, jag behöver också bli kursregistrerad. Det står att jag är kursanmäld på mina sidor men jag kan inte anmäla mig till KS1.

Tack på förhand.

@Alexander: Överlämnat till kursadministratören. Hon återkopplar.

Jag är inte kursregistrerad i kursen SF1626, fastän det står på mina sidor att jag har kursen! Jag behöver bli inskriven för att kunna göra omtentan i augusti!

Tyvärr finns det ingen på plats som kan registrera dig. Jag har skickat ett meddelande till kurssekreteraren om att du vill bli kursregistrerad och hon kommer återkoppla till dig när hon är tillbaka från semestern i början av augusti. 

Såg precis att hon har semester till den 12 augusti. Därför har jag lagt in dig bland plussarnas ansökningar. Om du har tur så får du en plats, annars är det reservplatserna som gäller för dig.

Ett tips: Om du i schemat här på social klickar på E31 så får du upp information om salen. Här är informationen.

En bra tumregel kan vara att kurser som börjar sin kurskod med ett "I" oftast examineras i Kista och kurser som börjar på andra bokstäver i sin kurskod än "I" oftast examineras på Campus Valhallavägen. 

Hej! Jag kan inte längre gå in och se mina resultat? När jag trycker på resultat så finns inte den sidan!

MVH MIchaéla

Det borde vara fixat nu.

Kommer inte in på resultatsidan...

Det fungerar fint för mig. Vilken typ av felmeddelande får du?

skulle inte resultatet vara uppe idag? jag har kollat både resultatsidan och ladok!

oj förlåt hitta det!

Hej,

Jag undrar när kompleteringen kommer att ske och hur kommer den att genomföras?

Ett epost-meddelande kommer inom kort gå ut till de som fått Fx med mer information om datum och sal.

I denna tråd finns lite allmän information om kompletteringstentan.

Efter att ha letat länge lyckades jag till slut hitta länken till statistiken för den här kursen. Vore utmärkt om den hamnade lite mer exponerat på den här sidan.

http://www.math.kth.se/math/GRU/2012.2013/SF162X-resultat/statistik/tentamina/SF1626_2013-05-27.html

Jag har nu lagt in en länk till statistiken till varje extenta på denna sida.

Min tentamen har inte blivit fullständigt rättad då uppgift 4,5 och 6 är glömda. Varför detta? Var vänder jag mig för hjälp?

Uppgifterna 4 och 5 är nämligen markerade med streck trots att jag har lämnat in svar på uppgifterna. Ni får se till att lägga in bedömning på dessa uppgifter senast imorgon.

Vad du ska göra då är att lämna in en begäran om omprövning på matematiks studentexpedition. Om du gör det imorgon (onsdag) så kommer du hinna få beslutet innan kompletteringstentan.

Tack för hjälpen. Jag överklagade idag då U4 och U5 ligger inlämnade i häftet men utan bedömning på lösningarna.